Распределение по величине скорости
Наряду с распределением по компонентам скорости в декартовых координатах (82.15), часто используется распределение в сферических координатах
где d W – элемент телесного угла, равный d W = sin q d q d j, (84.2)
если угловые координаты q и j выбраны, как показано на рис. 35. Распределение по величине скорости получается, если вероятность (84.1) проинтегрировать по телесному углу
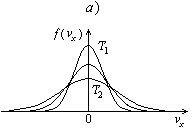
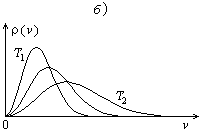
Графики плотности вероятности для распределений (82.15) и (84.3) представлены на рис. 36 (T 1 < T 2). Кривая плотности вероятности f (vx) (см. рис. 36, а) симметрична по отношению к положительным и отрицательным значениям vx, что является прямым следствием предположения о равноправности направлений молекулярного движения. Кривая r(v) (см. рис. 36, б) имеет максимум: наиболее вероятным состоянием молекулы является ее движение с отличной от нуля скоростью. Наиболее вероятная скорость равна
При повышении температуры доля быстрых молекул возрастает. Однако в соответствии с условием нормировки (82.13) площадь под кривой остается постоянной и равной единице. В любом случае доля очень быстрых молекул мала: и f (vx), и r(v) стремятся к нулю при стремлении величины аргумента к бесконечности.
|
, (84.1)
(84.3)
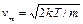. (84.4)
