Молекулярные пучки
В некоторых задачах необходимо рассчитать поток молекул, вылетающих из сосуда через малое отверстие, их распределение по скоростям в пучке. Такая необходимость возникает, в частности, при экспериментальной проверке распределения Максвелла. Малые размеры отверстия позволяют считать, что молекулярный пучок не нарушает состояния равновесия в сосуде. Тогда плотность потока молекул в пучке вычисляется по той же формуле, что и число молекул, падающих в единицу времени на единицу площади стенки. С учетом распределения по всем трем координатным направлениям в пространстве скоростей эта формула имеет вид
Последний результат записан в сферической системе координат. При интегрировании по углам (в пределах полусферы) получается плотность потока молекул с данной величиной скорости (в интервале v ¸ v + dv):
Интегральная плотность потока равна
где
Здесь
– распределение молекул в пучке по абсолютной скорости движения, а
– по направлениям движения. Помимо несущественной постоянной, распределение (86.5) отличается от максвелловского дополнительным множителем v. Его происхождение связано с тем, что быстрые молекулы вылетают из большего объема. Поэтому и средняя скорость, и средняя энергия молекул в пучке больше максвелловских средних:
Разница средних значений энергии молекулы в пучке и сосуде составляет kT / 2 и связана исключительно с поступательным движением молекул. Вращательная, колебательная энергии, энергия электронного возбуждения и другие виды энергии молекулы (если она ими обладает) могут не измениться при попадании молекулы в пучок. Поэтому, если средняя энергия молекулы в сосуде равна cVT, то в пучке она будет cVT + kT / 2 (cV – теплоемкость газа, рассчитанная на одну молекулу).
|

 . (86.1)
. (86.1) . (86.2)
. (86.2) , (86.3)
, (86.3)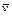 определяется соотношением (85.1). Нормированное распределение в пучке получится, если плотность потока молекул с данной скоростью, определяемую формулой (86.1), разделить на интегральную плотность потока (86.3):
определяется соотношением (85.1). Нормированное распределение в пучке получится, если плотность потока молекул с данной скоростью, определяемую формулой (86.1), разделить на интегральную плотность потока (86.3): . (86.4)
. (86.4)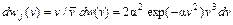 (86.5)
(86.5)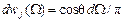 (86.6)
(86.6)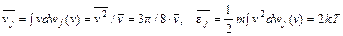 . (86.7)
. (86.7)


