Распределение Гиббса
Полученные выше распределения молекул по координатам и скоростям не зависят друг от друга. Поэтому вероятность того, что молекула находится в данном положении и одновременно имеет данную скорость, в соответствии с теоремой умножения вероятностей равна
где Можно ожидать, что более общее по сравнению с (90.1) распределение, применимое и к другим движениям молекулярной системы, будет иметь сходный вид
На такое предположение наталкивает аналогия между большим собранием квазинезависимых подсистем (например молекул разреженного многоатомного газа) и идеальным (одноатомным) газом. И в том и в другом случаях взаимодействие молекул-подсистем является слабым и не сказывается сколько-нибудь существенно на состоянии каждой подсистемы. В энергетическом балансе энергией взаимодействия можно пренебречь. Роль взаимодействия состоит в том, что оно вызывает переход подсистем из одних состояний в другие. Сам механизм взаимодействия не является существенным. В случае идеального газа вводится гипотеза о молекулярном хаосе, согласно которой все направления движения молекулы равновероятны, все ее положения в пространстве при одном и том же значении потенциальной энергии равноправны. Следствием гипотезы является независимость распределения вероятности состояний молекулы (90.1) от ее координат и скоростей. Эта вероятность полностью определяется энергией молекулы. Естественно ожидать, что и для произвольной квазизамкнутой (квазинезависимой, слабо взаимодействующей) подсистемы (в частности, для молекулы двухатомного газа) распределение вероятности состояний зависит только от ее энергии. Другими словами, состояния квазизамкнутой подсистемы с одной и той же энергией равновероятны (изменение направления движения, поворот при вращении и т. д. при неизменной энергии не сказываются на значениях вероятности). Это положение является естественным обобщением предположения о молекулярном хаосе в идеальном газе на случай более сложных систем. Оно приводит к появлению в распределении вероятности (90.2) экспоненциального множителя, а также определяет смысл и выражение для dГ. Вероятность обнаружить подсистему в одном из состояний с данной энергией, очевидно, пропорциональна числу таких (равновероятных) состояний. Состояние молекулы вполне характеризуется заданием ее обобщенных координат qi и импульсов pi и изображается в пространстве этих переменных (фазовом пространстве) точкой. Следовательно, число различных состояний молекулы с энергией e (в интервале e ¸ e + d e) пропорционально элементу объема фазового пространства. Данная цепочка рассуждений позволяет сделать вывод, что dГ должно быть элементом объема пространства обобщенных координат и импульсов (с точностью до независимого постоянного множителя), т. е.
Распределение (90.2) с таким определением dГ называется каноническим распределением Гиббса. Вопрос о том, каким должно быть dГ, и ответ на этот вопрос не столь уж просты. Для получения распределения Гиббса в статистической физике рассматривается ансамбль совершенно одинаковых по устройству квазизамкнутых подсистем, которые находятся в одном и том же макроскопическом состоянии, но, вообще говоря, различных микроскопических состояниях. Микросостоянию каждой подсистемы в фазовом пространстве (пространстве обобщенных координат и импульсов или Г -пространстве) отвечает точка. С течением времени микросостояние подсистемы изменяется (тогда как макроскопическое состояние остается неизменным) и изображающая точка прочерчивает в Г -пространстве фазовую траекторию. В соответствии с теоремой Лиувилля плотность изображающих точек в фазовом пространстве с течением времени для замкнутых систем не меняется (если же речь идет о квазизамкнутых подсистемах, то утверждение справедливо для не слишком больших промежутков времени, в течение которых подсистема с достаточной точностью ведет себя как замкнутая). Этот результат дополняется следующим предположением: все точки Г -пространства, принадлежащего гиперповерхности постоянной энергии замкнутой (изолированной) системы, равноправны. Это предположение дает микроканоническое распределение Гиббса. Из него для квазизамкнутой системы (подсистемы) следует каноническое распределение Гиббса. Это контуры более строгой теории. Легко проверить, что для случая идеального газа в однородном поле сил распределение Гиббса дает распределение Максвелла–Больцмана. Переход к каким-либо другим независимым переменным в распределении (90.2) делается обычным образом:
Якобиан этого преобразования определяет статистический вес в новых переменных. Более частный вид распределения (только по некоторым из переменных) получается в результате интегрирования по остальным переменным. Каноническое распределение Гиббса может быть обобщено на случай квантовых систем. Вероятность найти квантовую систему в состоянии с энергией e i равна
где Ω i (ε i) – число различных квантовых состояний системы с энергией e i (статистический вес, кратность вырождения уровня энергии). Нормировочная постоянная Z (статистическая сумма) находится суммированием по всему спектру энергии системы:
|

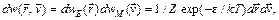
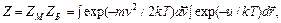 (90.1)
(90.1)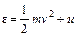 – полная энергия молекулы. Это распределение носит название распределения Максвелла–Больцмана. Им полностью определяется вероятность данного состояния молекулы, т. е. вероятность ее положения в шестимерном пространстве координат и скоростей. Однако это распределение связано только с поступательным движением молекулы и дает достаточную информацию лишь в случае одноатомного газа с нулевыми электрическими и магнитными моментами. Если же речь идет о двух- и многоатомных молекулах, то необходимы распределения, которые давали бы возможность определить вероятность того или иного поворота молекулы, величины ее вращательного момента, энергии колебательного движения и т. д.
– полная энергия молекулы. Это распределение носит название распределения Максвелла–Больцмана. Им полностью определяется вероятность данного состояния молекулы, т. е. вероятность ее положения в шестимерном пространстве координат и скоростей. Однако это распределение связано только с поступательным движением молекулы и дает достаточную информацию лишь в случае одноатомного газа с нулевыми электрическими и магнитными моментами. Если же речь идет о двух- и многоатомных молекулах, то необходимы распределения, которые давали бы возможность определить вероятность того или иного поворота молекулы, величины ее вращательного момента, энергии колебательного движения и т. д.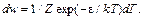 (90.2)
(90.2)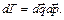 (90.3)
(90.3)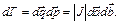
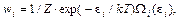 (90.4)
(90.4)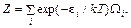 (90.5)
(90.5)


