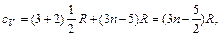Теплоемкость идеального газа. При создании теории теплоемкости большие успехи были достигнуты в результате применения распределения Гиббса.
При создании теории теплоемкости большие успехи были достигнуты в результате применения распределения Гиббса. Молярная теплоемкость газа вычисляется по известной средней энергии молекулы
Средняя энергия молекулы достаточно просто связана со статическим интегралом (суммой) Z:
т. е.
Таким образом, задача сводится к вычислению статистической суммы системы (в данном случае молекулы). Выше сказано, что теоретическое предсказание теплоемкости одноатомных газов хорошо подтверждается на опыте, и был установлен закон равнораспределения энергии по степеням свободы атомов. Для двухатомных газов все оказалось сложнее. Двухатомная молекула имеет шесть степеней свободы: три поступательных, две вращательных и одну колебательную. Энергия поступательного движения состоит из трех квадратичных слагаемых (соответствующих трем степеням свободы):
Статистическая сумма равна
так что Энергия вращательного движения состоит из двух квадратичных слагаемых (для двух степеней свободы):
где Mi (i = 1, 2) – моменты вращения вокруг осей, перпендикулярных оси молекулы и между собой; q и j – углы в сферической системе координат, определяющие ориентацию оси молекулы; p q и p j – соответствующие этим координатам обобщенные импульсы. Момент инерции J считается постоянным. Статистическую сумму можно вычислить, пользуясь тем или иным выражением для e вр:
или
Статистическую сумму можно получить также из выражения (91.8), устремляя a к нулю. Средняя энергия вращательного движения равна Энергия колебательного движения состоит из двух слагаемых (кинетической и потенциальной энергий), а степень свободы одна:
Здесь q – отклонение расстояния между атомами от равновесного значения a; рассматриваются малые колебания:
где n – частота колебаний. Средняя энергия осциллятора Пользуясь этим законом, можно рассчитать теплоемкость n- атомного газа. Его молекула имеет 3 n степеней свободы. Из них три степени свободы поступательные, две вращательные в случае линейных молекул и три для нелинейных молекул, остальные степени свободы колебательные. Вклад в теплоемкость каждой поступательной и вращательной степени свободы составляет R / 2, колебательной – R. В результате молярная теплоемкость газа в случае линейных молекул равна
для газа из нелинейных молекул
Однако, как будет показано ниже, вычисленные по этим формулам значения молярной теплоемкости нередко отличаются от значений, полученных в эксперименте.
|

 . (92.1)
. (92.1)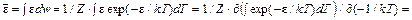

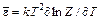 . (92.2)
. (92.2) . (92.3)
. (92.3)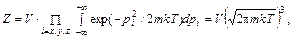 (92.4)
(92.4) . На каждую степень свободы поступательного движения молекулы приходится энергия kT / 2.
. На каждую степень свободы поступательного движения молекулы приходится энергия kT / 2. или
или 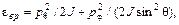 (92.5)
(92.5)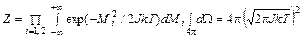 , (92.6)
, (92.6)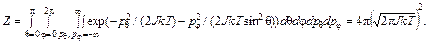
 , на каждую степень свободы приходится по kT / 2; cV = R.
, на каждую степень свободы приходится по kT / 2; cV = R. (92.7)
(92.7)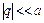 (приближение гармонического осциллятора); сила, стремящаяся вернуть атомы в равновесное положение, равна F = – c q; m – приведенная масса. Статистическая сумма осциллятора равна
(приближение гармонического осциллятора); сила, стремящаяся вернуть атомы в равновесное положение, равна F = – c q; m – приведенная масса. Статистическая сумма осциллятора равна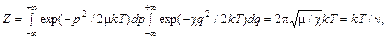 (92.8)
(92.8)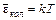 и теплоемкость cV = R. Для колебательного движения на одну степень свободы приходится энергия вдвое большая. Возникшее несоответствие закону равнораспределения было устранено путем изменения трактовки закона: каждое квадратичное слагаемое энергии имеет среднее значение, равное kT / 2.
и теплоемкость cV = R. Для колебательного движения на одну степень свободы приходится энергия вдвое большая. Возникшее несоответствие закону равнораспределения было устранено путем изменения трактовки закона: каждое квадратичное слагаемое энергии имеет среднее значение, равное kT / 2.