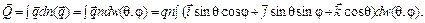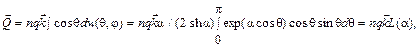Диэлектрические свойства газов
В качестве примера, иллюстрирующего применение распределения Гиббса, ниже рассматривается явление поляризации газа, состоящего из полярных (дипольных) молекул (рис. 39).
Дипольный момент молекулы определяется выражением
где суммирование ведется по всем зарядам частицы. В атомах и молекулах, обладающих симметричной формой (к ним относятся молекулы H2,O2, CH4 и др.), положительные и отрицательные заряды расположены симметрично. Все эти частицы не имеют собственного дипольного момента. Сильно асимметричные молекулы, например представляющие образование из двух разных ионов, такие как HCl, HBr и т. д., или молекулы, имеющие асимметричную форму, такие как CH3Cl, H2O и т. д., обладают дипольным моментом и в отсутствие электрического поля. Для простоты считается, что молекулы газа – твердые ротаторы (жесткие двухатомные молекулы), обладающие постоянным собственным дипольным моментом q=e(r 1 + r 2), где r 1 и r 2 – расстояния атомов от центра тяжести молекулы (m 1 r 1 = m 2 r 2), e – величина их разноименных зарядов (рис. 39). Молекула имеет массу m = m 1 + m 2 и момент инерции J = m 1 r 12 + m 2 r 22. Энергия молекулы (в системе центра тяжести) равна сумме энергий вращательного движения составляющих масс:
и потенциальной энергии, зависящей от ориентации диполя в постоянном внешнем электрическом поле напряженности E,
Потенциальная энергия, как видно из формулы (91.2), выражается через угол q между осью диполя и полем, а ориентация молекулы определяется двумя сферическими координатами q и j. Эти переменные естественно выбрать в качестве обобщенных координат. В данной системе координат молекула может быть полностью представлена с помощью единичного радиуса-вектора
где
Из механики известно, что при произвольном выборе обобщенных координат qi и соответствующих им скоростей
где
Обобщенный импульс pj имеет смысл момента вращения вокруг оси Z (при этом
Теперь можно конкретизировать распределение Гиббса. Оно принимает вид
Постоянная Z легко находится из условия нормировки:
Z = 8π2 JkT · shα / α, (91.8)
где α = qE / kT. При получении выражения для Z (91.8) использованы равенства
Если распределение (91.7) проинтегрировать по p q и по p j, то с учетом равенства (91.8) будет получена вероятность данной ориентации диполя:
Это распределение позволяет рассчитать равновесную поляризацию газа (суммарный дипольный момент молекул в единице объема):
(91.10)
Вследствие осевой симметрии среднее значение азимутальной составляющей дипольного момента молекул единицы объема равна нулю. Поэтому
(91.11)
где L (a) = cth a – 1 / a – функция Ланжевена, α = qE / kT. Таким образом, равновесная поляризация газа направлена вдоль поля и ее величина является сложной функцией напряженности и температуры. Электрическое поле стремится ориентировать молекулярные диполи вдоль вектора напряженности. Тепловое движение препятствует этому (в отсутствие поля молекулы ориентированы беспорядочно). Насколько эффективно упорядочивающее действие поля, зависит от параметра a, выражающего отношение потенциальной энергии молекулы к тепловой. При a >> 1 (большие поля, низкие температуры) функция L (a)» a / 3, так что Q = c E (c = nq 2 / (3 kT) – диэлектрическая восприимчивость, или поляризуемость газа). Дипольный момент многих молекул (HCl, H2O и др.) имеет порядок 10 – 18 эл.-ст. ед. × см. Поэтому величина a весьма мала при всех температурах, при которых газы еще не конденсируются, и во всех практически достижимых полях. Чтобы параметр a был порядка единицы, напряженность поля должна иметь величину E» 104× T В / см. При комнатной температуре это значение равно E» 3×106 В / см, что практически недостижимо. Таким образом, в реальных условиях ориентирующее действие поля является слабым. Это соответствует линейному росту поляризации с напряженностью поля. Для поляризуемости c имеет место обратно пропорциональная зависимость от температуры (закон Кюри).
|


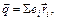
 где
где 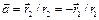 , (91.1)
, (91.1)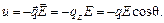 (91.2)
(91.2) (91.3)
(91.3) – единичные векторы по осям x, y, z соответственно. Если соотношение (91.3) продифференцировать по времени и результат подставить в формулу (91.1), то для e вр получится следующее выражение через обобщенные скорости
– единичные векторы по осям x, y, z соответственно. Если соотношение (91.3) продифференцировать по времени и результат подставить в формулу (91.1), то для e вр получится следующее выражение через обобщенные скорости 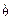 и
и 
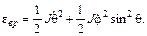 (91.4)
(91.4)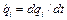 обобщенные импульсы pi могут быть определены по формуле
обобщенные импульсы pi могут быть определены по формуле
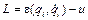 – функция Лагранжа, e и u – соответственно кинетическая и потенциальная энергии. В рассматриваемом случае
– функция Лагранжа, e и u – соответственно кинетическая и потенциальная энергии. В рассматриваемом случае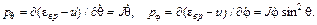 (91.5)
(91.5)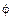 есть угловая скорость, атомы находятся на расстояниях r 1sin q и r 2 sin q от оси Z; естественно, p j зависит от угла q). Аналогичный смысл имеет p q. Это момент вращения вокруг оси, перпендикулярной плоскости, проходящей через ось Z и мгновенное положение оси диполя. Полная энергия молекулы выражается через обобщенные координаты и импульсы следующим образом:
есть угловая скорость, атомы находятся на расстояниях r 1sin q и r 2 sin q от оси Z; естественно, p j зависит от угла q). Аналогичный смысл имеет p q. Это момент вращения вокруг оси, перпендикулярной плоскости, проходящей через ось Z и мгновенное положение оси диполя. Полная энергия молекулы выражается через обобщенные координаты и импульсы следующим образом: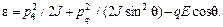 (91.6)
(91.6)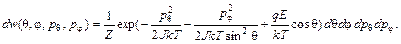 (91.7)
(91.7)

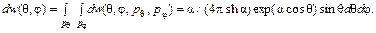 (91.9)
(91.9)