Распределение Больцмана. Из опыта известно, что газ в отсутствие внешнего поля равномерно распределен по объему сосуда
Из опыта известно, что газ в отсутствие внешнего поля равномерно распределен по объему сосуда. Это дает основание считать, что все части объема V сосуда равноправны и вероятность обнаружить молекулу в элементе объема dV = dxdydz около точки с координатами x, y, z равна
dw (x, y, z) = dV / V = dxdydz / V. (89.1)
Между тем на практике часто приходится иметь дело с газом, находящимся в потенциальном внешнем поле. Важным примером такого поля является поле тяжести. Молекула газа в этом поле обладает потенциальной энергией, равной u = mgz, (89.2)
где ось z направлена вертикально вверх. Наличие силы тяжести приводит к тому, что давление газа меняется с высотой. Вес газа в сосуде измеряется разностью давлений, оказываемых газом на дно и крышку сосуда:
P =(p (0) – p (h)) S. (89.3)
В создании этой разности участвуют все молекулы газа, хотя большая часть из них непосредственно ни с дном, ни с крышкой сосуда не сталкивается. С другой стороны, вес газа равен просто весу всех его молекул:
Таким образом, для веса газа имеются два выражения: (89.3) и (89.4). Приравнивание их друг другу дает интегральное уравнение
Это уравнение справедливо для любых h, поэтому его можно записать в виде
Дифференцирование (89.6) по z приводит к дифференциальному уравнению
Если газ идеальный и температура его не меняется с высотой, то (89.7) сводится к dn/dz = – mg/kT · n. (89.8)
Решение этого уравнения определяет изменение концентрации молекул с высотой: n (z) = n (0) exp(– mgz/kT). (89.9)
Концентрация молекул у дна сосуда и полное их число N связаны условием нормировки
Параметр a = mgh / kT характеризует неоднородность распределения газа по высоте. При a >> 1 неоднородность значительна: энергия теплового движения недостаточна, чтобы молекулы могли подняться высоко, и они сосредоточены ближе к дну сосуда. При a << 1 из выражения для N следует, что n (0) = N / Sh, т. е. распределение близко к однородному. Можно ввести характеристическую длину распределения молекул в поле тяжести (из условия a = 1) hk = kT / mg. (89.11)
Для условий земной атмосферы hk» 10 км. Сооружаемые емкости имеют значительно меньшие габариты, поэтому неоднородность распределения паров в них не наблюдается. Лишь при подъеме в горы или с помощью авиации обнаруживается влияние поля тяжести на распределение воздуха в атмосфере. Необходимо подчеркнуть, что формула (89.9) применима только к изотермической "тонкой" атмосфере. Из нее следует барометрическая формула p (z) = p (0) exp (– mgz / kT). (89.12)
Воздух представляет собой смесь газов, молекулы которых имеют различную массу. В соответствии с формулой (89.9) состав атмосферы должен резко изменяться с высотой:
n' / n'' = n' (0) / n'' (0)exp((m'' – m') gz / kT). (89.13)
Здесь одним штрихом отмечены величины, относящиеся к легкой компоненте, двумя – для тяжелой. Из полученного соотношения следует, что относительная концентрация легких газов должна увеличиваться с высотой. Измерения состава воздуха на разных высотах не подтвердили этого вывода. Интенсивная конвекция в пределах тропосферы приводит к известному выравниванию состава воздуха по высоте. Общеизвестно также падение температуры с высотой. Атмосфера Земли не находится в состоянии статистического равновесия. Распределению (89.9) можно придать несколько иной вид. Вероятность обнаружить молекулу в слое толщиной dz на высоте z определяется долей таких молекул от общего числа:
dw (z) = dN (z) / N = n (z) Sdz / N = 1/ Z exp(– u (z) / kT) Sdz, (89.14)
где u – потенциальная энергия молекулы, вычисляемая по формуле (89.2); Z = N / n (0) – нормировочный множитель. В произвольной системе координат распределение (89.14) будет иметь вид
где
u = – g mM / r. (89.16)
Тогда с учетом сферической симметрии
dw (r) = 1 / Z exp(g mM / kTr)) 4p r 2 dr; (89.17)
Для концентрации молекул (если не задаваться вопросом о величине Z) из распределения (89.17) следует формула
n (r) =
При z = r – r 0 << r 0 из формулы (89.19) получается распределение для тонкой атмосферы. Действительно, r – 1 – r 0–1 @ – z / r 02, g M / r 02 = g – ускорение свободного падения. В результате, из формулы (89.19) следует распределение (89.9). Казалось бы, все хорошо, но есть одна неприятность: интеграл в выражении для Z (89.18) расходится и Z =¥. Нельзя равновесным образом распределить конечное число молекул в бесконечном пространстве. На больших высотах плотность газа очень мала, молекулы почти не сталкиваются, и там не устанавливается равновесное состояние. Распределение Больцмана можно использовать, чтобы найти распределение взвесей в суспензиях и эмульсиях. Мельчайшие частицы взвесей находятся в непрерывном хаотическом движении, почти не сталкиваясь друг с другом. Тепловой характер их движения имеет молекулярно-кинетическую природу. Он вызван различием в импульсах, получаемых частицей в результате столкновений с молекулами растворителя. Потенциальная энергия частицы взвеси равна
u = mgz (1 – ρ0 / ρ), (89.20)
где r и r0 – плотности вещества частицы и растворителя соответственно. Выражение (89.20) написано с учетом выталкивающей силы. Для концентрации частиц получается распределение, аналогичное (89.9):
Оно было использовано Перреном для экспериментального определения числа Авогадро (и тем самым постоянной Больцмана). Растирая гуммигут в воде, Перрен получал эмульсию ярко-желтого цвета, в которой при наблюдении в микроскоп можно было различить множество зернышек сферической формы. Перрен получал эмульсию также другим способом, растворяя гуммигут в спирте, а затем разбавляя раствор большим количеством воды. Многократное центрифугирование давало весьма однородную эмульсию, состоящую из шарообразных частиц радиусом порядка микрона. Обработав 1 кг гуммигута, Перрен через несколько месяцев получил фракцию, содержащую несколько десятых доли грамма зерен желаемого размера. С этой фракцией и были выполнены описываемые здесь опыты и опыты по броуновскому движению. К предметному стеклу микроскопа приклеивалось очень тонкое стекло с просверленным в нем широким отверстием. Получалась плоская ванночка (кювета Цейса), глубина которой была около 100 мкм (0,1 мм). В центре ванночки помещалась капля исследуемой эмульсии, которая сплющивалась покровным стеклом. Чтобы избежать испарения, края покровного стекла покрывались парафином или лаком. Тогда препарат можно было наблюдать в течение нескольких дней или недель. Количественные измерения были выполнены, когда препарат помещался горизонтально, а микроскоп – вертикально. Объектив был очень сильного увеличения с малой глубиной фокуса. Одновременно можно было видеть только частицы в слое глубиной порядка микрона. Фокусируя микроскоп на разные глубины, можно было сосчитать число видимых броуновских частиц в разных слоях и определить отношение концентраций этих частиц. Разность высот измерялась микрометрическим винтом микроскопа. Специальным образом определялся размер зерен – диаметр их был около 0,37 мкм. Определенные таким образом значения постоянной Больцмана и числа Авогадро оказались в хорошем согласии с результатами других экспериментов. Эти опыты Перрена, а также его опыты по броуновскому движению, ставшие классическими, были выполнены в 1908–1911 гг. и имели большое значение для утверждения атомистики. Неоднородность в распределении частиц молекулярного размера удается создать с помощью центрифуги. Центрифугирование нашло широкое применение в химии и биологии как эффективный способ разделения близких по молекулярному весу или плотности веществ. В лабораторной системе отсчета газ в центрифуге вращается как единое целое, стало быть, имеется центростремительное ускорение, т. е. система не находится в равновесии и к ней нельзя применить распределение Больцмана. В системе же отсчета, связанной с центрифугой, объект исследования находится в равновесии, и к нему можно применить указанное распределение. Но в этой системе отсчета на частицы действует центробежная сила. Соответствующая потенциальная энергия частицы равна
Распределение Больцмана с учетом цилиндрической симметрии имеет вид
где l – высота барабана центрифуги. Для концентрации частиц получена формула
Из формулы следует, что концентрация тяжелых частиц у боковой стенки центрифуги относительно выше, что используется для разделения смесей.
|

 . (89.4)
. (89.4)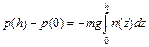 . (89.5)
. (89.5)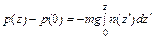 . (89.6)
. (89.6)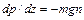 . (89.7)
. (89.7)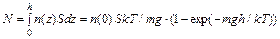 . (89.10)
. (89.10)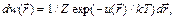 (89.15)
(89.15)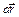 – элемент объема конфигурационного пространства. Это и есть распределение Больцмана. Его можно использовать, чтобы найти распределение газа в "толстой" изотермической атмосфере. В этом случае потенциальная энергия молекулы равна
– элемент объема конфигурационного пространства. Это и есть распределение Больцмана. Его можно использовать, чтобы найти распределение газа в "толстой" изотермической атмосфере. В этом случае потенциальная энергия молекулы равна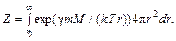 (89.18)
(89.18)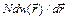 = N / Z exp(γ mM / (kTr)) = n (r 0) exp(γ mM / (kT)(r –1 – r 0–1)). (89.19)
= N / Z exp(γ mM / (kTr)) = n (r 0) exp(γ mM / (kT)(r –1 – r 0–1)). (89.19)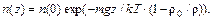 (89.21)
(89.21) (89.22)
(89.22)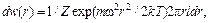 (89.23)
(89.23) (89.24)
(89.24)


