Теплоемкость газа во внешнем силовом поле
На этом затруднения теории не заканчиваются. В присутствие внешних полей на поступательные и вращательные степени свободы приходится не только кинетическая, но и потенциальная энергия, и соответствующие слагаемые не являются квадратичными. Так, для одноатомного газа в сосуде высотой h, находящемся в поле тяжести, статистическая сумма равна
Множитель перед интегралом связан с кинетической энергией молекулы, а интеграл – с потенциальной. Для средней энергии получается равенство
При низких температурах параметр α = mgh / kT >> 1 и При повышении температуры теплоемкость падает, и при α << 1 она равна 3 R / 2. Газ в этом случае равномерно распределен по объему сосуда. Причина падения теплоемкости с ростом температуры заключается в ограниченности координатного пространства размерами сосуда. Аналогичная ситуация наблюдается и в рассмотренном ранее случае газа во внешнем электрическом поле. При повышении температуры газа степень ориентированности его дипольных молекул уменьшается, увеличивается их потенциальная энергия. Однако это увеличение энергии небеспредельное. При высоких температурах дипольные молекулы ориентированы равномерно по всем направлениям, дальнейшее повышение температуры не приводит к увеличению потенциальной энергии молекул. Таким образом, потенциальная энергия молекул газа во внешнем поле при низких температурах постоянна и не зависит от специфики поля, а при высоких температурах влияние поля исчезает из-за ограничений на объем фазового пространства.
|

 (95.1)
(95.1) (95.2)
(95.2)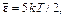 т. е. имеется дополнительное слагаемое kT, связанное с потенциальной энергией молекулы. Соответственно этому cV =5 R / 2, а не 3 R / 2. Распределение газа в сосуде неравномерное. Чтобы повысить температуру газа, нужно подвести к нему дополнительное количество теплоты – оно расходуется на работу молекул против силы тяжести и увеличение их потенциальной энергии.
т. е. имеется дополнительное слагаемое kT, связанное с потенциальной энергией молекулы. Соответственно этому cV =5 R / 2, а не 3 R / 2. Распределение газа в сосуде неравномерное. Чтобы повысить температуру газа, нужно подвести к нему дополнительное количество теплоты – оно расходуется на работу молекул против силы тяжести и увеличение их потенциальной энергии.


