Распределение по скоростям относительного движения
Итак, установление равновесия, теплопередача и т. д. – все эти процессы осуществляются в результате взаимодействия молекул. При этом молекулы не слишком плотных газов в некотором приближении можно считать упругими шариками. Ставится задача определения частоты их столкновения. Если
Из механики известно, что движение двух частиц с массами m 1 и m 2 можно разложить на движение их общего центра тяжести со скоростью
и относительное движение. Скорости частиц
Движение центра тяжести не играет роли в проблеме столкновения. А относительное движение происходит так, как если бы одна из частиц была неподвижной, а вторая имела массу, равную приведенной массе
(рассматривается двухчастичное столкновение). Сложение этих двух уравнений дает условие постоянства скорости центра масс:
Если уравнения движения разделить на массы частиц и вычесть затем одно из другого, то для относительного движения получится уравнение
или
В системе отсчета, связанной с какой-либо молекулой, движение остальных молекул хаотично, и следует ожидать, что распределение их по относительным скоростям будет максвелловским (только вместо массы молекулы в него будет входить приведенная масса):
Этот результат можно получить непосредственно, вычисляя вероятность того, что первая молекула имеет скорость
где распределения Если затем перейти от независимых векторов
Поскольку якобиан перехода равен
то рассматриваемое распределение распадается на два независимых
откуда следует распределение (98.4). Формально распределение (98.4) отличается от (82.16) только массой. Поэтому для средней скорости относительного движения можно сразу же написать
Если массы сталкивающихся молекул одинаковы, то
|

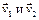 – скорости двух молекул, то для столкновения важны не сами по себе эти скорости, а скорость относительного движения молекул
– скорости двух молекул, то для столкновения важны не сами по себе эти скорости, а скорость относительного движения молекул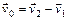 . (98.1)
. (98.1) (98.2)
(98.2) следующим образом:
следующим образом: (98.3)
(98.3) . Это следует непосредственно из законов Ньютона. Уравнения движения частиц имеют вид
. Это следует непосредственно из законов Ньютона. Уравнения движения частиц имеют вид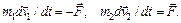


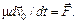
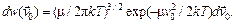 (98.4)
(98.4)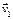 , а вторая –
, а вторая – 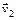 :
: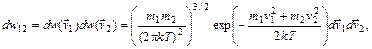 (98.5)
(98.5)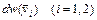 максвелловские. Молекулы имеют произвольные (независимые) скорости, поэтому при выводе (98.5) используется теорема умножения вероятностей.
максвелловские. Молекулы имеют произвольные (независимые) скорости, поэтому при выводе (98.5) используется теорема умножения вероятностей.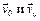 и ввести вместо масс молекул приведенную массу
и ввести вместо масс молекул приведенную массу  то
то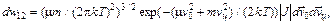 (98.6)
(98.6)
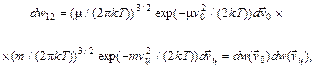 (98.7)
(98.7) (98.8)
(98.8)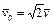 .
.


