Измерение автономного риска: среднеквадратическое отклонение
Чтобы быть полезной для практического использования, любая мера риска должна иметь точное определение – нам необходима мера «сжатости» распределения вероятности. Одной из таких мер является среднеквадратическое (стандартное) отклонение (СКО) – обозначается Таблица 5.3 Вычисление среднеквадратического отклонения для компании «М»
Стандартное отклонение = 1. Вычисляем среднюю доходность: Средняя доходность = Мы уже выяснили ранее, что для компании «М» k = 15%. 2. Вычисляем отклонение каждого отдельного значения доходности ki от её среднего значения k: Отклонение = ki-k. 3. Возводим в квадрат каждое отклонение и взвешиваем полученные квадратические отклонения в соответствии с их вероятностями. Итогом является вариация доходности, как это показано в столбце 3 таблицы (формула 5.2): Вариация = 4. Наконец, извлекая из вариации квадратный корень, получаем среднеквадратическое отклонение (формула 7.3): Среднеквадратическое отклонение = Таким образом, среднеквадратическое (стандартное) отклонение доходности – это в определенном смысле средневзвешенное отклонение от её ожидаемого значения, и оно показывает, насколько выше или ниже ожидаемой окажется вероятная фактическая доходность. Среднеквадратическое отклонение для компании «М» согласно таблице 5.3, составляет
Рис. 5.2. Диапазоны вероятности при нормальном распределении Таким образом, компания «М» имеет большее среднеквадратическое отклонение доходности, что указывает на большую вероятность того, что средняя доходность не будет достигнута. Следовательно, вложение в компанию «М» вне какого-либо портфеля является более рискованным. Если распределение вероятностей нормальное, или гауссовское то в 68,26% случаев фактическая доходность окажется в интервале
|

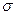 . Чем меньше квадратическое отклонение, тем более распределение вероятности «сжато» и соответственно тем ниже риск акций. Чтобы вычислить среднеквадратическое отклонение, мы выполняем действия, представленные в таблице 5.3.
. Чем меньше квадратическое отклонение, тем более распределение вероятности «сжато» и соответственно тем ниже риск акций. Чтобы вычислить среднеквадратическое отклонение, мы выполняем действия, представленные в таблице 5.3. 7,225 = 2167,5
7,225 = 2167,5
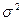 = 4335
= 4335
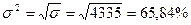
 P1k1 + P2k2+ …+ Pnkn =
P1k1 + P2k2+ …+ Pnkn = 
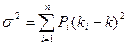 . (5.2)
. (5.2) (5.3)
(5.3)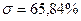 . Выполняя тот же расчёт, находим, что среднеквадратическое отклонение для компании «А» составляет 3,87%.
. Выполняя тот же расчёт, находим, что среднеквадратическое отклонение для компании «А» составляет 3,87%.
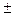 1 её СКО от среднего значения. На рисунке 5.2 отражен именно этот эффект. Кроме того, на рисунке также показаны и вероятности того, что доходность окажется в интервалах
1 её СКО от среднего значения. На рисунке 5.2 отражен именно этот эффект. Кроме того, на рисунке также показаны и вероятности того, что доходность окажется в интервалах 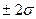 и
и 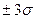 от среднего значения. Для компании «М» k = 15% и
от среднего значения. Для компании «М» k = 15% и 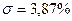 . Таким образом, если два распределения доходности этих акций нормальны, то с вероятностью существует 68,26% фактическая доходность компании «М» будет находиться в диапазоне 15
. Таким образом, если два распределения доходности этих акций нормальны, то с вероятностью существует 68,26% фактическая доходность компании «М» будет находиться в диапазоне 15 


