Расчет средней доходности: матрица выигрышей
Вычисление предполагаемой нормы прибыли можно также выразить с помощью формулы, которая демонстрирует те же вычисления, что и таблица матрицы выигрышей: (формула 5.1)
Ожидаемая доходность актива равна (формула 5.1): где
Ожидание доходности компании «А» также составляет 15%:
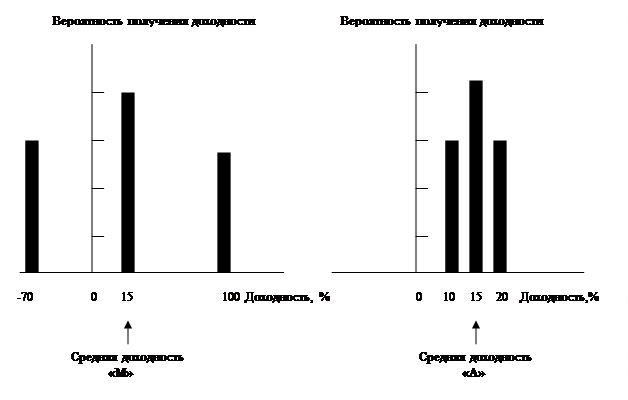
Диапазон доходности компании «М» составляет от –70% до +100%, при ожидании доходности на уровне 15%. Ожидаемая прибыль компании «А» составляет также 15%, но при этом диапазон её вероятностей значительно уже. Необходимо учитывать, что пока мы предполагали, что могут реализоваться лишь три исхода: высокий, средний и ограниченный спрос на продукцию компаний. Разумеется, в реальной жизни спрос может колебаться от глубокой депрессии до фантастического бума, и между этими граничными возможностями существует бесконечное множество промежуточных исходов. Если бы у нас хватило бы времени и терпения, чтобы приписать вероятность каждому отдельному уровню спроса, а также найти доходность акций для каждого уровня спроса, то у нас бы получилась таблица, аналогичная таблице 5.1, за исключением того, что в каждом её столбце было бы гораздо больше записей. Эту таблицу можно было бы также использовать для вычисления ожиданий доходности, а вероятности различных уровней доходности можно было бы изобразить на графике с помощью непрерывных распределений, аналогичным представленным на рис. 5.1. Приводя график (рис.5.1), мы несколько изменили наши изначальные предположения, посчитав, как и прежде, что существует практически нулевая вероятность того, что доходность акций компании «М» будет ниже -70 или выше 100% (доходность акций компании «А» будет ниже 10 или выше 20%), но теоретически возможен любой результат. Понятно, что эта гипотеза более реалистична, чем прежняя.
Рис. 5.1. Непрерывные распределения вероятности доходности акции компаний «М» и «А» Чем более «сжатым» будет график распределения вероятности, тем ближе окажется фактическая доходность к ожидаемой и, следовательно, тем меньше вероятность, что действительная прибыль окажется значительно ниже предполагаемой. Таким образом, чем более «сжато» распределение вероятности, тем ниже риск, задаваемый акции. Поскольку у компании «А» распределение вероятности весьма сжато, её фактическая доходность с большей вероятностью будет близка к ожидаемым 15%, чем доходность компании «М».
|

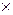 100 =30%
100 =30%
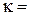 15%
15%
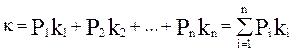 (5.1)
(5.1)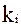 - это один из возможных исходов (i – его номер),
- это один из возможных исходов (i – его номер), 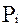 - вероятность этого исхода, а n – общее число возможных исходов. Таким образом,
- вероятность этого исхода, а n – общее число возможных исходов. Таким образом, 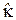 - это средневзвешенное значение доходности, при этом весом каждого отдельного её значения
- это средневзвешенное значение доходности, при этом весом каждого отдельного её значения 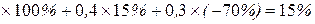 .
.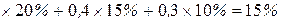 .
.