Понятие бета-коэффициента
Как отмечалось выше, основной вывод из анализа модели ценообразования капитальных активов (САРМ) заключается в том, что релевантный риск отдельных акций — это тот риск, который эти акции привносят в хорошо диверсифицированный портфель ценных бумаг. Поэтому доходность диверсифицированного портфеля акций должна сравниваться с доходностью рыночного портфеля — портфеля, включающего все акции, присутствующие на рынке. Следовательно, мера релевантного риска отдельных акций, которая называется бета-коэффициентом, определяется, согласно модели САРМ, как количество риска, которое акции привносят в рыночный портфель. Если обозначить через riM корреляцию между доходностью i-й акции и доходностью рынка в целом, через
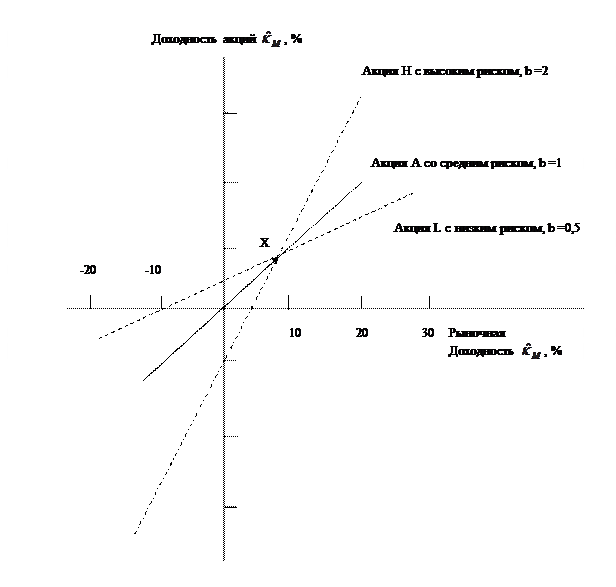
Данное выражение показывает, что акции с высоким риском В калькуляторах и электронных таблицах для вычисления бета-коэффициентов обычно используется формула (5.7), но можно предложить и другой способ. Отложим по оси х графика доходность рынка в целом, а по оси у — отдельных акций, как показано на рис. 5.7. Тогда бета-коэффициент будет показывать силу тенденции к движению акций вверх и вниз вместе с рыночным портфелем. Акции со средним риском определяются как акции, которые растут и падают в той же мере, что и рынок в целом. Такие акции имеют бета-коэффициент, равный единице, что указывает на то, что в общем случае, если рыночный индекс поднимется на 10%, и эти акции также поднимутся в цене на 10%, а при его падении на 10% и стоимость этих акций также упадет на 10%. Если b = 0,5, то акции будут вдвое менее волатильны по сравнению с рынком — они будут подниматься и опускаться в цене в среднем вдвое медленнее рынка в целом, а портфель, содержащий такие акции, будет наполовину менее рискованным, чем портфель, содержащий акции с бета-коэффициентом, равным единице. Наконец, если b = 2,0, акции будут в два раза более неустойчивы, чем рынок в целом, а портфель, содержащий их, будет в два раза более рискованным, чем средний портфель.
Рис. 5.7. Относительная волатильность доходности акций Н, А, L На рис. 5.7, в сравнении с доходностью рынка (рыночного портфеля) в целом, схематично изображена доходность трех типов акций: Н (с высоким коэффициентом (b = 2) и высоким риском), А (с риском, равным среднерыночному и b = 1) и L (с низким риском и b = 0,5). Видно, что все типы акций двигались в том же направлении, что и рыночный портфель, состоящий из всех активов, но доходность акций с высоким риском колебалась сильнее рыночной, акций со средним риском — примерно так же, как и рыночная, а доходность акций с низким риском оказалась наиболее устойчивой. Таким образом, если: b < 1, то акции только менее рискованны по сравнению с рынком в целом; b = 1, то акции имеют среднерыночный риск; b > 1, то акции более рискованны, чем в среднем на рынке. Отметим, что портфель, состоящий из ценных бумаг с низким бета-коэффициентом, сам будет иметь низкий бета-коэффициент, поскольку бета-коэффициент портфеля является средневзвешенным значением бета-коэффициентов акций, входящих в его состав (формула 5.8):
Здесь bр — это бета-коэффициент портфеля из п акции, wi — доля стоимости портфеля, приходящаяся нa i- ю акцию; bi — бета-коэффициент i -й акции. Например, если инвестор имеет портфель стоимостью 100 тыс. ден.ед., состоящий поровну из инвестиций в три типа акций, и если бета-коэффициенты этих акций будут равны соответственно 0,7, 0,9 и 1,1, то бета-коэффициент портфеля будет bр = 0,9: bр = 0,333 х 0,7 + 0,33 × 0,9 + 0,333 х 1,1 = 0,9. Бета-коэффициенты вычисляются 0,33 × 0,9 публикуются рядом компаний и множеством других организаций буквально для тысяч компаний. Большинство акций имеет бета-коэффициенты в пределах от 0,50 до 1,50, а среднее их значение для всех акций по определению равно 1,0. Теоретически возможно, чтобы у акции был отрицательный бета-коэффициент. В этом случае доходность данной акции будет стремиться вырасти в те периоды, когда доходность по другим акциям будет снижаться. Однако на практике никогда не встречались акции с отрицательным бета-коэффициентом. Тем не менее, следует помнить, что в отдельные годы акции могут двигаться в направлении, противоположном движению рынка, даже если бета-коэффициент акций положителен. Если акции имеют положительный бета-коэффициент, мы можем, лишь ожидать, что доходы по ним возрастут по мере роста рынка акций в целом. Однако факторы, характерные для отдельных компаний, могут вызвать снижение фактической доходности отдельных акций даже в те годы, когда на рынке в целом наблюдался рост. Вычисление бета-коэффициентов является достаточно трудоемкой задачей. Это обусловлено тем, что модель ценообразования капитальных активов САРМ — это модель, рассчитывающая доходности активов — ожидаемые или требуемые инвесторами в будущем доходности. Все ее переменные представляют собой прогнозируемые, а не фактические значения. В частности, бета-коэффициент, используемый инвесторами, отражает ожидаемую рискованность доходности данной акции по сравнению с рынком в целом. Однако на практике можно рассчитывать бета-коэффициенты, используя фактические данные за прошедшие периоды, и затем предполагать, что риск акций в будущем будет такой же, каким он был в прошлом.
|

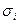 — среднеквадратическое отклонение доходности акции и через
— среднеквадратическое отклонение доходности акции и через 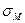 — СКО доходности рынка, то, как доказывается в литературе по САРМ, бета-коэффициент i-й акции, обозначаемый bi, можно вычислить следующим образом (формула 7.7):
— СКО доходности рынка, то, как доказывается в литературе по САРМ, бета-коэффициент i-й акции, обозначаемый bi, можно вычислить следующим образом (формула 7.7):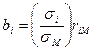 (5.7)
(5.7)

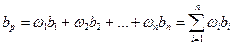 (5.8)
(5.8)


