Соотношение между доходностью и риском
В предыдущем разделе мы увидели, что, согласно теории модели ценообразования капитальных активов (САРМ), бета-коэффициент является мерой релевантного риска акций. Теперь мы должны установить соотношение между риском и доходностью: какая рисковая премия будет достаточна инвесторам для принятого ими на себя риска, измеряемого с помощью бета-коэффициента? Для этого сначала введем несколько обозначений:
ki— требуемая инвесторами доходность акции. Понятно, что если ki больше
kRF— безрисковая доходность (норма прибыли). В данном контексте kRF обычно будет означать доходность долгосрочных облигаций Казначейства; bi — бета-коэффициент i-й акции. Напомним, что для акций А со «средним» риском бета-коэффициент равен bA - 1,0;
RPM = (
Премия за риск рыночного портфеля (рыночный риск) зависит от степени несклонности инвесторов к риску. Если в данный момент облигации Казначейства приносят доходность, равную kRF = 6%, а рыночный портфель имеет доходность RP Если нам известна премия за рыночный риск RPM, а также риск акции, измеренный с помощью ее бета-коэффициента bi, то мы можем найти премию за риск акции как их произведение: Премия за риск акции i = RPi = Формулу для требуемой инвесторами доходности любого вложения можно записать так: Требуемая доходность = Безрисковая ставка + Рисковая премия. Здесь безрисковая ставка доходности включает в себя премию за предполагаемую инфляцию, причем предполагается, что изучаются активы, имеющие одинаковые сроки до погашения и ликвидность. В этих условиях соотношение между требуемой доходностью актива и риском можно графически представить линией рынка ценных бумаг (SML). Требуемую доходность акции i можно в этом случае выразить следующим образом (уравнение SML): Требуемая доходность акции i = Безрисковая ставка + +Рыночная премия за риск х Бета-коэффициент акции, или
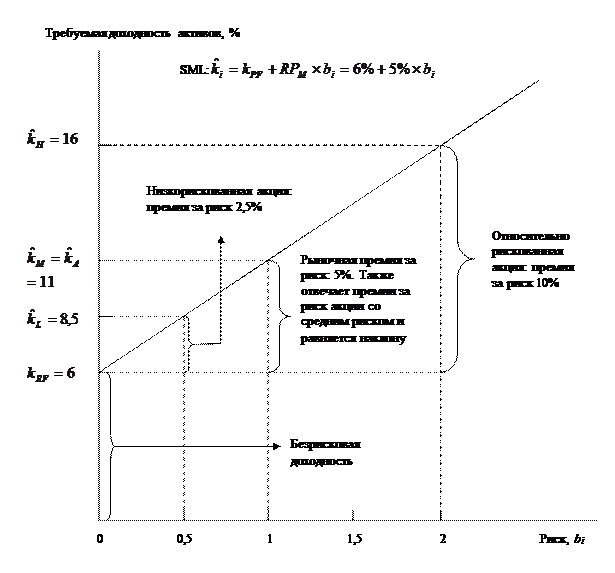
Если акция j более рискованна, чем i, и имеет бета-коэффициент bi- = 2,0, то требуемая доходность по акции j составит 16%:
Для акции А со средним по рынку риском, у которых b = 1,0, требуемая доходность 11%, — т. е. будет такой же, как и для рыночного портфеля:
Как уже отмечалось выше, уравнение (5.9) называется уравнением линии рынка ценных бумаг (SML). Эта линия при kRF = 6% и
Рис. 5.8. Линия рынка ценных бумаг (SML) Отметим при этом следующие важные моменты. 1. Требуемые инвесторами доходности активов откладываются по вертикальной оси, в то время как риск, измеряемый с помощью бета-коэффициента, откладывается по горизонтальной оси. 2. Для безрисковых активов бета-коэффициент равен единице, — следовательно, kRF рис. 5.8представляется как точка пересечения SML с вертикальной осью. Если бы мы могли составить портфель ценных бумаг, у которого бета-коэффициент был бы нулевым, его требуемая доходность была бы равна безрисковой. 3. Наклон линии SML (5% на рис. 5.8) отражает среднюю степень несклонности инвесторов криску — чем больше несклонность среднего инвестора к риску, тем: а) круче наклон линии, б) больше премия за риск акций и в) тем выше требуемая инвесторами доходность для всех рисковых активов. И линия рынка ценных бумаг, и положение компании на ней изменяются с течением времени вследствие изменений процентных ставок и бета-коэффициентов отдельных компаний, несклонности инвесторов к риску. Подобные эффекты будут рассмотрены в последующих разделах.
|

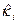 — ожидаемая инвесторами (на ближайшие периоды) средняя доходность i -й акции;
— ожидаемая инвесторами (на ближайшие периоды) средняя доходность i -й акции;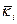 — реализованная в прошлом периоде фактическая доходность акции. Человек, естественно, не знает, какова она окажется по итогам наступающего периода, когда он рассматривает вопрос о приобретении акций в его начале;
— реализованная в прошлом периоде фактическая доходность акции. Человек, естественно, не знает, какова она окажется по итогам наступающего периода, когда он рассматривает вопрос о приобретении акций в его начале;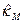 — требуемая инвесторами доходность рыночного портфеля ценных бумаг — портфеля, состоящего из всех акций, присутствующих на рынке. kM одновременно представляет собой также и требуемую доходность акции со средним риском;
— требуемая инвесторами доходность рыночного портфеля ценных бумаг — портфеля, состоящего из всех акций, присутствующих на рынке. kM одновременно представляет собой также и требуемую доходность акции со средним риском; RPi. = (
RPi. = (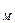 =
= 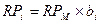 . Например, если
. Например, если 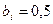 и RPM = 5%, то RPi составляет 2,5%:
и RPM = 5%, то RPi составляет 2,5%: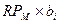 = 5%
= 5% 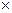 0,5% = 2,5% (5.9)
0,5% = 2,5% (5.9)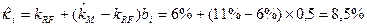 (5.10)
(5.10)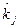 = 6% + (11%-6%)
= 6% + (11%-6%) 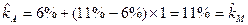 .
.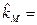 11% представлена в графической форме на рис. 5.8.
11% представлена в графической форме на рис. 5.8.