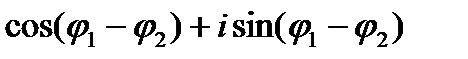Формула деления комплексных чисел в тригонометрической форме
Возьмем два комплексных числа в тригонометрической форме.
Используя формулу деления комплексных чисел вида
получим для наших двух комплексных чисел формулу:
/учитывая основное тригонометрическое тождество, согласно которому = ( /используя тригонометрические свойства косинуса и синуса суммы и разности/ =
Таким образом, для нахождения частного z1/z2 следует модуль числа z1 разделить на модуль числа z2, а из аргумента числа z1 вычесть аргумент числа z2
|

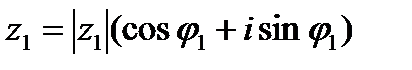
 , где z 2≠0.
, где z 2≠0.
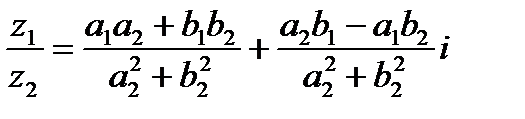 ,
,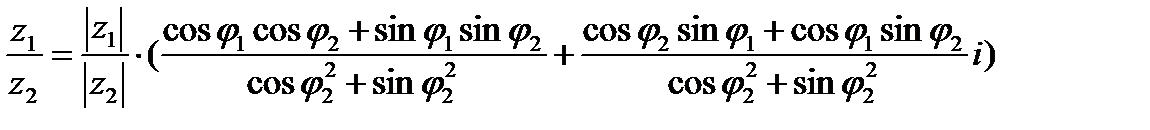 =
=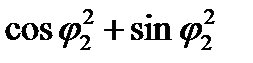 =1/
=1/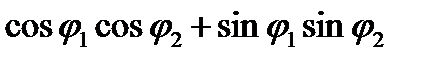 )+ (
)+ (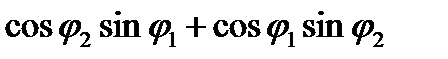 ) i =
) i =