Изменение матрицы линейного преобразования при замене базиса.
А’=T-1AT Пусть А – матрица линейного преобразования f в базисе Предположим, что мы переходим к новому базису, в котором преобразованию отвечает новая матрица А’, а Т есть матрица перехода от исходного базиса к новому базису. Х=ТХ’, где Х – столбец из старых координат разложенного по базису вектора, а Х’ – столбец из новых координат. Аналогично Y=TY’ Учитывая, что Y=AX, Х=ТХ’ и Y=TY’, установим связь между Х’ и Y’. Y’=T-1Y=T-1AX=T-1ATX’ Отсюдаследует, что матрицей отображения А в новом базисе будет матрица A’=T-1ATX, чтд.
|

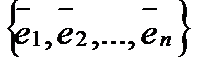 .
.


