Линейная независимость лестничной системы векторов.
Предложение: любая лестничная система векторов линейно независима. Доказательство: Предположим противное. Тогда один из данных векторов должен линейно выражаться через остальные. Пусть, например, а линейно выражается через b, c,…, то есть
Но такое равенство невозможно, поскольку первая координата вектора а отлична от нуля, а первая координата вектора Полученное противоречие доказывает, что линейная система векторов линейно независима.
4. Однозначность разложения вектора по базису. Предложение: Координаты вектора в данном базисе определены однозначно. Допустим,что существуют два способа разложения вектора а по базису Тогда И Если вычесть эти два равенства, получим, что
Так как векторы базиса линейно независимы, то они не равны нулю. Значит, То есть k=l, и существует лишь один способ разложения вектора по базису.
|
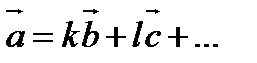
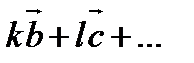равна нулю (из определения лестничной системы векторов первая координата всех последующих векторов равна нулю).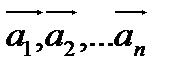
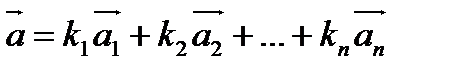
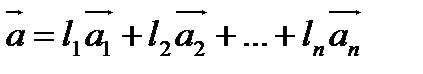
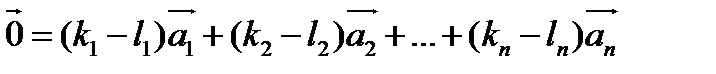
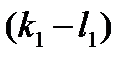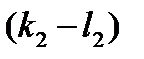=0, 
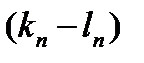=0, …, 
=0
