Существование бесконечного числа решений у системы линейных однородных уравнений, в которой число неизвестных больше числа уравнений.
Однородная система, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение. Запишем общий вид однородной системы m уравнений с n неизвестными:
а21х1+ а22х2+…+ а2nхn=0 … аm1х1+ аm2х2+…+ аmnхn=0, где n>m Применим к системе метод Гаусса. В процессе преобразований не могут получиться противоречивые уравнения
т.к. все свободные члены уравнений – нули. Значит, после некоторого числа шагов мы получаем систему, где каждому уравнению будет соответствовать свое базисное неизвестное. Но поскольку число уравнений меньше числа неизвестных, то и число базисных неизвестных должно быть меньше числа неизвестных. Следовательно, обязательно имеются свободные неизвестные, а система имеет бесчисленное множество решений.
|
а11х1+ а12х2+…+ а1nхn=0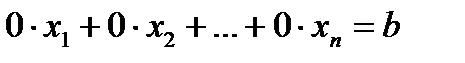
, где b ≠0,
