Общее уравнение плоскости.
Ax + By + Cz + D = 0 (2) Вектор N {A,B,C}называется нормальным вектором к плоскости (2) или (1).
3.0.3.5.3. Особые случаи уравнения Ax + By + Cz + D = 0: I. D = 0, Ax + By + Cz = 0 – плоскость проходит через начало координат. II. C = 0, Ax + By + D = 0 – плоскость параллельна оси Oz. III. C = D = 0, Ax + By = 0 – плоскость проходит через ось Oz. IV. B = C = 0, Ax + D = 0 – плоскость параллельна плоскости yOz. V. Уравнения координатных плоскостей: x = 0, y = 0, z = 0.
3.0.3.6. Уравнение плоскости в отрезках на осях, смысл его коэффициентов.
3.0.3.7. Уравнение плоскости, проходящей через три различные точки пространства. Пусть r1 (x1, y1, z1), r2 (x2, y2, z2), r3 (x3, y3, z3) – радиус-векторы точек M1, M2, M3 и r (x, y, z) - радиус-вектор текущей точки M, тогда уравнение плоскости, проходящей через эти точки можно записать в виде равенства нулю смешанного произведения: (r - r1) (r2 - r1) (r3- r1) = 0 или через определитель в координатной форме:
(x2 - x1) (y2 - y1) (z2 - z1) =0 (x3- x1) (y3- y1) (z3- z1) 3.0.3.8. Угол образованный двумя плоскостями. cos j = ± где N { A,B,C } и N1 { A1,B1,C1 } - нормальные векторы к плоскостям Ax + By + Cz + D = 0 и A1 x + B1 y + C1 z + D1 = 0 Условие параллельности плоскостей:
Условие перпендикулярности плоскостей:
AA1 + BB1 + CC1 = 0
3.0.3.9. Расстояние d точки M0 (x0, y0, z0) от плоскости Ax + By + Cz + D = 0: d = здесь N { A,B,C } - нормальный к плоскости вектор.
3.0.3.10. Уравнение прямой.
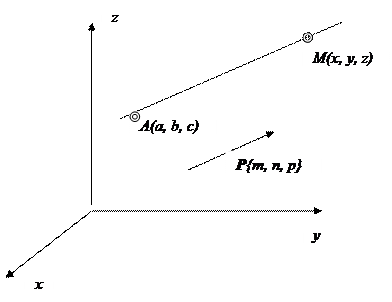
3.0.3.10.1. Уравнение прямой,проходящей через точку A(a,b,c) и параллельной вектору P {m, n, p}. Пусть M(x, y, z) – произвольная точка прямой,
Уравнения (1) называются каноническими уравнениями прямой. Вектор P {m, n, p} называется направляющим вектором прямой.
3.0.3.10.2. Параметрические уравнения прямой получим, приравняв каждое из отношений (1) параметру t:
y = n t + b (2) z = p t + c
3.0.3.10.3. Уравнения прямой,проходящей через две точки:
3.0.3.10.4. Общие уравнения прямой:
Ax + By + Cz + D = 0 (4) A1 x + B1 y + C1 z + D1 = 0
3.0.3.10.5. Уравнения прямой в проекциях получим, исключив из общих уравнений (4) один раз y, другой раз x:
y = n z + b (5) Уравнения (5) можно записать в канонической форме:
|



 (x - x 1) (y - y1 ) (z - z1 )
(x - x 1) (y - y1 ) (z - z1 )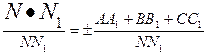
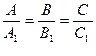

 тогда, AM || P и по условию параллельности векторов
тогда, AM || P и по условию параллельности векторов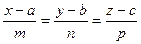 (1)
(1)
 x = m t + a
x = m t + a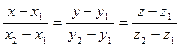 (3)
(3)
 x = m z + a
x = m z + a



