Условие расположения двух прямых
в одной плоскости:
m n p =0 m1 n1 p1
---------------------------------------------------------------------------------------------------
3.1. Матрицы и определители, системы линейных уравнений. 72. Проверить совместность системы уравнений X1 + 5X2 = 1 X1 + 5X2 = 7 73. Методом Гауса решить систему уравнений X1 + 2X2 + 5X3 = -9 X1 - X2 + 3X3 = 2 3X1 - 6X2 - X3 = 25 74. Перемножить матрицы. Проверить некоммутативность (AB ¹ BA)
-1 3 - 2 1 75. Проверить ассоциативность произведения трех матриц (AB)C = A(BC), добавив к двум матрицам предыдущего примера любую третью. 76. Найти к первой матрице предыдущего примера обратную. 77. Составить любую неединичную матрицу а) первого; b) второго; c) третьего; d) четвертого порядка и вычислить ее определитель. 78. Решить систему уравнений примера 73 (метод Гауса) а) методом обратной матрицы; b) правилом Крамера.
3.2.Векторная алгебра.
79. 80. Построить точку М {5;-3;4} и определить длину и направление ее радиус-вектора. 81. Определить угол между векторами a = -i + j и b = i – 2 j + 2 k. 82. Определить вектор c = a´ b, если 1) a = 3 i, b = 2 k; 2) a = i + j, b = i – j. 83. Вычислить объем параллелепипеда, построенного на векторах a = 3 i + 4 j, b = - 3 j + k, c = 2 j + 5 k. 3.3. Прямая и плоскость. 84. Даны точки М1(0,-1,3) и М2(1,3,5). Написать уравнение плоскости,
85. Найти угол плоскости, проходящей через точки O(0,0,0), M1(a,-a,0), M1(a,a,a), с плоскостью xOy. 86. Найти след прямой 87. Написать уравнение плоскости, проходящей через параллельные прямые 88. Определить угол между прямыми: y = 2x-3 и y = ----------------------------------------------------------------------------------------------------
|
, 
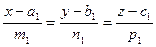
a - a 1 b - b1 c - c1
4 9 1 -3
По сторонам ОА (3 см) и ОВ (4 см) прямоугольника ОАСВ отложены единичные (1см) векторы i и j. Выразить через i и j векторы ОА, АС, СВ, ВО, ОС и ВА.
проходящей через точку М1 и перпендикулярной к вектору N = М1М2 ..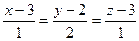
на плоскости xOz, положив в уравнениии прямой y = 0.
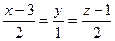и 
.
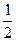x+ 1.
