Уравнение прямой в отрезках на осях.
где a и b – величины отрезков, отсекаемой прямой на осях координат.
3.0.3.3. Угол между прямыми. Условие параллельности и перпендикулярности двух прямых. 3.0.3.3.1. Угол j, отсчитанный против часовой стрелки от прямой y = k1 x + b1 до прямой y = k2 x + b2, определяется формулой tg j = Для прямых, заданных уравнениями A1 x + B1 y + C1 = 0 и A2 x + B2 y + C2 = 0, формула (1) принимает вид tg j = Условие параллельности: k1 = k2 или Условие перпендикулярности: k2 = - 3.0.3.3.2. Уравнение прямой, проходящей через две данные точки A (x1, y1) и B (x2, y2):
3.0.3.3.3. Расстояние d точки M0(x0,y0) от прямой Ax + By + C = 0: d =
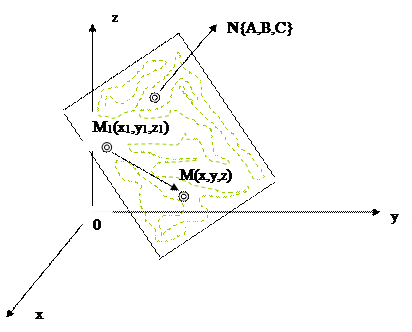
3.0.3.4. Понятие об уравнении поверхности в пространстве. Уравнение поверхности как геометрического места точек. Уравнением поверхности называется уравнение с переменными x, y и z которому удовлетворяют координаты любой точки этой поверхности и только они. Входящие в уравнение поверхности переменные x, y и zназываются текущими координатами, а буквенные постоянные – параметрами. Например, в уравнении сферы (радиуса R с центором в начале координат) x2 + y2 + z2 = R2 переменные x, y и z – текущие координаты, а постоянная R – параметр. Чтобы составить уравнение поверхности как геометрического места точек, обладающих одинаковым свойством, нужно: 4) взять произвольную (текущую) точку М (x,y,z) поверхности, 5) записать равенством общее свойство всех точек М этой поверхности, 6) входящие в это равенство отрезки (и углы) выразить через текущие координаты точки М (x, y, z) и через данные задачи.
3.0.3.5. Общее уравнение плоскости, смысл его коэффициентов.
3.0.3.5.1. Уравнение плоскости, проходящей через точку М1(x1, y1, z1) и перпендикулярной к вектору N {A,B,C}
A(x - x1) + B(y - y1) + C (z -z1) = 0 (1)
|

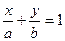 (3)
(3)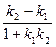 (1)
(1)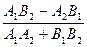
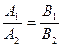
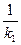 или A1 A2 + B1 B2 = 0
или A1 A2 + B1 B2 = 0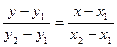
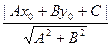
 ПустьМ(x, y, z) – произвольная точка плоскости. Тода М1М ^ N и по условию перпендикулярности векторов
ПустьМ(x, y, z) – произвольная точка плоскости. Тода М1М ^ N и по условию перпендикулярности векторов