Свойства смешанного произведения векторов
Для любых векторов 1) При перестановке местами двух множителей смешанное произведение меняет знак:
2) При циклической перестановке множителей смешанное произведение не меняется:
3) Если
4)
5) Абсолютная величина смешанного произведения векторов равна объему параллелепипеда, построенного на этих векторах
Объем пирамиды, построенный на тех же векторах в 6 раз меньше:
Таким образом, скалярное произведение используют для нахождения длин и углов, векторное произведение – для вычисления площадей, а смешанное – для нахождения объемов.
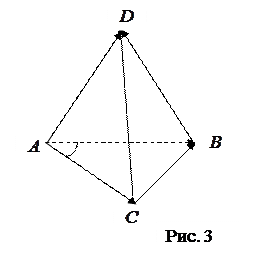
Пример 6. (Образец выполнения задачи 4 из контрольной работы). Даны вершины пирамиды:
a) длину ребра b) угол между ребрами c) площадь грани d) объем пирамиды.
Решение. a) Найдем вектор
b) Угол между ребрами
Следовательно, c)
d) Возьмем три вектора, на которых построена пирамида, например,
Значит,
|

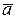 ,
, 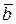 и
и 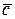 справедливо:
справедливо: ,
, 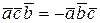 ,
, 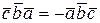
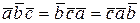 .
. ,
, 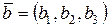 ,
,  , то
, то .
.

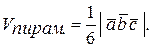
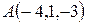 ,
, 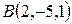 ,
,  и
и 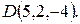
 Найти:
Найти: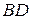 ;
; и
и  ;
; ;
;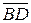 , а затем его норму. Это и будет длина ребра
, а затем его норму. Это и будет длина ребра  ,
, 
 и
и 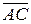 (рис. 3), используя формулу:
(рис. 3), используя формулу: .
.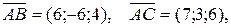
 .
.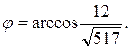
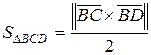 ,
, 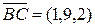 ,
, 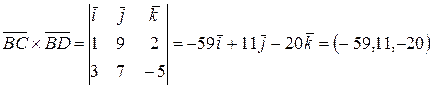
 ,
,  .
. ,
, 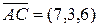 и
и  , и найдем их смешанное произведение:
, и найдем их смешанное произведение: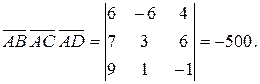
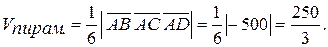 n
n


