Свойства векторного произведения
Для любых векторов для любых 1. 2. 3. 4.
5. Таблица умножения ортов:
6. Если
Векторное произведение часто используют для нахождения площадей.
Пример 5. Найти площадь треугольника с вершинами Решение. Найдем координаты векторов
Учитывая, что норма векторного произведения векторов
Таким образом,
|
, 
, 
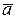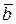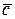и для любого числа 
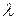справедливо:
;
;
;
;
, 
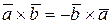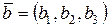, то
, 
, 
.
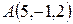и 
(напомним, что для этого нужно из координат конца вектора вычесть координаты начала):
, 
,
.n
