2.1. Пространства 
Обозначим через  множество упорядоченных наборов по
множество упорядоченных наборов по  действительных чисел:
действительных чисел:  ,
, 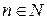 . Сами такие наборы называются
. Сами такие наборы называются  - мерными векторами.
- мерными векторами.
Рассмотрим  -мерные векторы
-мерные векторы  и
и 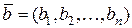 . Два вектора
. Два вектора 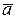 и
и 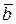 называются равными, если равны их соответствующие координаты:
называются равными, если равны их соответствующие координаты:  ,
, 
Введем на множестве  линейные операции.
линейные операции.
Суммой двух векторов 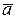 и
и 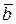 называется вектор, координаты которого равны суммам соответствующих координат векторов
называется вектор, координаты которого равны суммам соответствующих координат векторов 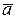 и
и 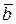 :
:
 .
.
Произведением вектора 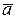 на действительное число
на действительное число 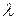 называется вектор, координаты которого равны произведению числа
называется вектор, координаты которого равны произведению числа 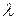 на соответствующие координаты вектора
на соответствующие координаты вектора 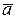 :
:
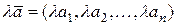 .
.
Линейные операции над векторами удовлетворяют свойствам:
1. 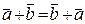 5.
5. 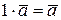
2. 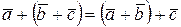 6.
6. 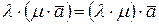
3.  7.
7. 
4. 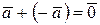 8.
8. 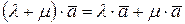
где 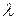 ,
, 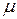 - произвольные действительные числа,
- произвольные действительные числа,  - нулевой вектор,
- нулевой вектор, 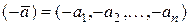 – вектор, противоположный к вектору
– вектор, противоположный к вектору 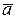 .
.
Множество  , с введенными на нем линейными операциями, называется пространством
, с введенными на нем линейными операциями, называется пространством  .
.
Если линейные операции удовлетворяют указанным выше восьми свойствам, то соответствующее пространство называется линейным или векторным пространством. Таким образом, пространство  является векторным пространством.
является векторным пространством.
Заметим, что элементами некоторых пространств могут быть не только векторы, но и различные другие объекты. Так, например, линейным пространством является множество всех квадратных матриц одинакового размера (объясните почему!). Несложно показать, что линейным будет пространство всех алгебраических многочленов степени, не превышающей натурального числа  (проверьте выполнение свойств 1-8). В тоже время, множество всех многочленов фиксированной степени не является линейным пространством, т.к. сумма двух таких многочленов может оказаться многочленом более низкой степени.
(проверьте выполнение свойств 1-8). В тоже время, множество всех многочленов фиксированной степени не является линейным пространством, т.к. сумма двух таких многочленов может оказаться многочленом более низкой степени.


 действительных чисел:
действительных чисел:  ,
, 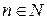 . Сами такие наборы называются
. Сами такие наборы называются 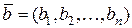 . Два вектора
. Два вектора 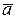 и
и 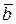 называются равными, если равны их соответствующие координаты:
называются равными, если равны их соответствующие координаты:  ,
, 
 .
.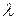 называется вектор, координаты которого равны произведению числа
называется вектор, координаты которого равны произведению числа 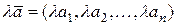 .
.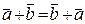 5.
5. 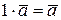
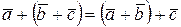 6.
6. 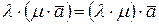
 7.
7. 
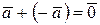 8.
8. 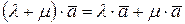
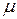 - произвольные действительные числа,
- произвольные действительные числа,  - нулевой вектор,
- нулевой вектор, 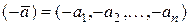 – вектор, противоположный к вектору
– вектор, противоположный к вектору 


