Зависимость вероятности оценки стимула от его физической характеристики (длины) в третьем эксперименте с жесткой инструкцией в 2-категориальной системе ответов.

S_0,25 = 650, S₀,₅₀ (Md) = 900, S_0,75 = 1125 – верхний и нижний квартили и медиана психометрической кривой в условиях либеральной инструкции.

С помощью графика 3.2 находятся следующие пороговые показатели: Точка субъективного равенства (PSE) = 900, Константная ошибка (CE) = 0, Интервал неопределенности (IU) = 335, Дифференциальный порог (DL) = 167,5.

Апроксимация экспериментально полученных точек кривой недостаточно точна, т.к. по 5 точкам мы воспроизводим форму психофизической кривой. Получается, что точность оценки порога зависит от того, насколько хорошо мы воспроизвели по этим 5 точкам форму психофизической кривой. Поэтому обработка данных включает в себя третий способ – способ нормальной интерполяции. При этом мы делаем допущение, что наша психофизическая функция является функцией нормального распределения. Масштаб оси ординат выражается в единицах стандартного отклонения этого распределения (т.е. в так называемых нормальных или z-координатах), психометрическая функция, имеющая в предыдущих графиках S-образную форму в линейных координатах, превращается в прямую линию. Далее аналогично, как и при построении предыдущих графиков, находятся интересующие экспериментатора параметры прямой. Для этого необходимо преобразовать пропорции ответов P с помощью таблиц нормального распределения в значения Z, представляющие собой нормированные по стандартному отклонению расстояния от стимульных точек до медианы. Перевод вероятностей субъективной оценки стимула в z – оценки осуществляется с помощью специальной “таблицы перевода значений p в значения z”. Берутся значения P (>), полученные при переводе из 3-категориальной системы в 2-категориальную. По пяти экспериментальным точкам с помощью регрессионного анализа проводится наилучшая прямая, проходящая через эти точки. По оси Y при построении графика задается z-оценки (зависимая переменная), по оси X – интенсивность сравниваемого стимула (независимая переменная).Связь между стандартной случайной величиной Z и экспериментальной случайной величиной X (субъективная величина стимула) является линейной, так как Z и X связаны уравнением прямой = 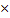X - , где m – среднее, δ (сигма) – стандартное отклонение. По сути, уравнение линейной прямой y=аx+b и 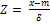означают одно и то же, только вторая формула является преобразованной. Вычислив коэффициенты a и b линейной функции y=аx+b, можно будет найти неизвестные «х» по известным «y» (z=0, z=1, z=-1). Шкала z-оценок представляет собой шкалу единиц стандартного отклонения – δ. Точка z=0 соответствует нулевому отклонению от среднего (медианы), точки z=1 или -1 – отклонению от среднего на 1 δ вправо или влево. Если точки на графике разбросаны недалеко от регрессионной прямой – гипотеза о наличии функциональной связи подтверждается. Под графиками приведены результаты регрессионного анализа, с помощью которого в дальнейшем вычислялись уравнения регрессионной прямой (уравнение вида y=аx+b, где угловому коэффициенту (a) соответствует значение «b1» из результатов регрессионного анализа, а свободному члену (b)– значение «константы»).