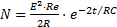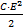Важным преимуществом формулы в отличие от графиков, таблиц и статистических данных является то, что они допускают проведение различных математических операций.
Подобрав общее уравнение для кривой, можно с успехом применять дифференцирование и интегрирование. Пример: Батарея конденсаторов имеет эффективную емкость 1000мкф и должна заряжаться через сопротивление 1000ом до напряжения постоянного тока 1000в. Резистор сопротивлением 10000ом помещен в водяной калориметр для измерения на нем энергии Постоянная времени RC равна 10 сек. Было проведено несколько измерений напряжения на конденсаторе и на резисторе: С= f(t) и R=f(t). Результаты нанесены на график (полулогарифмическая бумага). С помощью соответствующих преобразований определены (получены0 следующие функции: eR =E℮- t / RC и eC = E(1-℮- t / RC); где: eR – напряжение на резисторе; eC –напряжение на конденсаторе; t – время от момента включения в в цепь; Е – приложенное напряжение (1000в); R – сопротивление резистора (10000ом); С – емкость конденсатора (1000·10-6ф). Количество энергии. накапливаемое на резисторе равно:
И, окончательно, общая энергия равна При заданных величинах общая энергия равнаN = 0,5·1000·10 -6 ·1000 2= 500дж = 119,5кал. (для сведения: фарада = (кулон)2 / джоуль) В данном эксперименте через резистор сопротивлением 10000 ом будет протекать ток равный 1000ф /10000 ом = 0,1 А. и поэтому резистор может быть небольшим. Если калориметр, в который помещен резистор, содержит 30 г воды, то ее температура увеличится на 2,8˚с и можно вычислить количество накопленной энергии. Математический анализ экспериментальных данных будет наиболее успешным, если исследователь имеет некоторое представление о том, что можно ожидать и в каком направлении следует двигаться. Если не знать, что (e2R / R)dt представляет собой мгновенное значение энергии, рассеиваемой на конденсаторе, то он не может правильно выполнить интегрирование; с другой стороны, маловероятно, что дифференцирование кривой e = f(t) принесет какую-либо пользу, если в эксперименте есть какая ни будь ошибка.
|

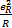 ,а общее количество энергии, рассеиваемое на резисторе за бесконечное время (t→∞), равно:
,а общее количество энергии, рассеиваемое на резисторе за бесконечное время (t→∞), равно: , после интегрирования
, после интегрирования