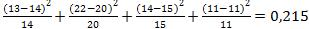Эти члены образуют Пуассоновский ряд .сумма членов которого равна 1.
При: т<1 вероятность максимальна при нулевом числе событий. 1<т<2 вероятность максимальна при появлении одного события. Для проверки на соответствие пуассоновскому распределению обычно вычисляется каждый член ряда и с помощью χ2- критерия эти члены сравниваются с членами эмпирического ряда. Для приближенной инженерной прикидки можно использовать проверку с помощью графиков – аналогично тому, как проверка на «нормальность» выполнялась с помощью вероятностной бумаги. Если не принимать во внимание член е-т , выражающий отсутствие событий, то: Фактическое число ожидаемых интерваловЕпвремени (или участков) дляп -го члена определяется выражением:
или ln (En∙ n!) =C1 n + С2. (6) где: С1 – постоянная;С1 = lnm; C2 – постоянная, С2 = (ln N –m). Ни С1, ни С2 не зависят от номера п (номера члена). Формула 6 – уравнение прямой в отрезках. Таким образом: если необходимо проверить, является ли данное распределение пуассоновским, то вычислять m (среднее число событий в интервале) не надо. Достаточно умножить наблюдаемое число En на каждое значение п! и отложить полученные результаты на логарифмической шкале,а на линейной шкале отложить п. Если график зависимости Е п п! от п представляет собой прямую (или близкую к ней), то можно предположить, что рассматриваемый ряд является пуассоновским. *Эмпирическое распределение –результат наблюдений (форма таблицы чисел, гистограммы, в которой указывается, какое число раз переменная принимала определенные значения. Пример:В течение 2х месяцев (60дней) велось наблюдение на перекрестке. Данные наблюдений
Предположим: Данные случайные и образуют пуассоновский ряд Вопрос:Справедливо ли такое предположение для этих данных Решение:Построим график зависимости En∙n! от п. Проведенные вычисления представим в виде таблицы:
Первые 4е точки вблизи прямой, 5я – отклонение вверх. Отдельные отсчеты могут иметь отклонения. Нижние значения (на графике) – наиболее значимые, и свидетельствуют о хорошем соответствии пуассоновскому распределению. Более строгую проверку проведем с помощью χ2- критерия Среднее число событий равно т = R / N= 87 / 60 = 1,45, где: R= 1·22+ 2·14+3·7+4·4 =87 Рис. 13. График зависимости En∙n! от п. Зная т по формуле 5 можно вычислить значения En для каждого п. Получаем: Результаты представлены в таблице:
*предсказанные значения En округлены до ближайшего целого.
Число степеней свободы равно 3. На графике χ2 = f(число степеней свободы) видно, что вероятность этого (или большего0 значения χ2 составляет ~ 0,99. Т.о. гипотеза о том, что выборки данных относятся к одной и той же совокупности, является почти достоверной. Итак: Результаты проверки с помощью χ2- критерия соответствуют результатам приближенной графической проверки.
Графический анализ данных.
|

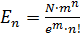 . (5) или ln En= n ln m + ln N – m – ln п!
. (5) или ln En= n ln m + ln N – m – ln п!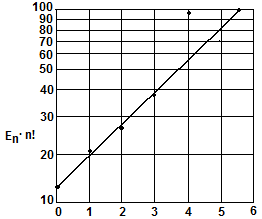 Строим график зависимости En∙n! от п (рис.13)
Строим график зависимости En∙n! от п (рис.13)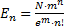 =
= 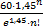
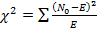 =
=