Метод наименьших квадратов
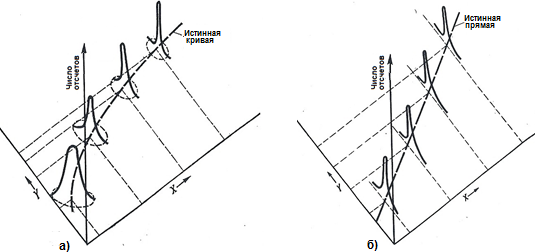
Большое значение имеют научные аспекты графического анализа: - относительная точность переменных, наносимых на график; - исключение резко отклоняющихся значений; - выбор наиболее удачных шкал; - построение наилучшей прямой Самый строгий и точный способ построения на плоскости ХУ наилучшей прямой (или прямой корреляции) по некоторой группе точек - метод наименьших квадратов. Допустим, что как независимая переменная Х, варьируемая в некотором интервале, так и зависимая переменная У имеют случайную ошибку, которая больше при малых значениях этих величин, и уменьшается с их увеличением. Задавая все возможные значения Х и многократно считывая значения У, получим бесконечную совокупность экспериментальных точек, заполняющих область значений (Х,У) и имеем бесконечное множество двумерных нормальных распределений переменной У. Построив для каждого интервала зависимость величины отклонения от числа отсчетов получим распределение (рис.14а):
Рис.14. а) - График зависимости величины отклонения от числа отсчетов для каждого интервала; б) - График одинаковых нормальных распределений при многократном снятии 4х показаний, лежащих на прямой при условии: только переменная У имеет случайную ошибку, которая одинакова для всех значений У. При нормальном распределении ошибок измерительного прибора,как известно, сумма квадратов отклонений показаний от наилучшего значения минимальна. Это положение справедливо и для рассматриваемого общего случая – бесконечного множества кривых нормального распределения (см. рис.14). Т.о. наилучшая линия, проходящая через множество точек, рассеянных на плоскости ХУ, должна занимать положение, при котором сумма квадратов отклонений точек от этой линии минимальна. Если при многократном снятии 4х точек (ожидается, что они лежат на истинной кривой) переменные Х и У имеют неопределенность или случайную ошибку, уменьшающуюся при увеличении Х иУ, то получаются двумерные нормальные распределения, изображенные на графике. Именно это правило и объясняет происхождение термина «метод наименьших квадратов». Классическая задача наименьших квадратов Известно: 1.Бесконечная совокупность точек на плоскости ХУ дает прямую.
|