Число значащих цифр выбирается исходя из результатов анализа неопределенности.
Если неопределенность измерения составляет 10%, то в лучшем случае можно указать не более двух значащих цифр: такой отсчет, как 98, означает, что результат заключен между 97 и 99. Но в то же время он может с вероятностью 10% находиться между 95 и 101. При неопределенности равной 1% можно указать 3 цифры, при 0,1% - 4 цифры и т.д. При обработке данных ошибки определенным образом комбинируются. Если допустить небрежность, можно потерять значащие цифры. Предположим: вес образца до испытаний на коррозию - 1,54кг, после испытаний – 1,52кг. Потеря веса – 0,02кг. При испытании 2го образца потеря – 0,02кг. Сравнивая два результата ясно, что нужны весы, которые позволяют получить 4, а то и 5 значащих цифр. Если имеем большой объем обработки данных с применением технических средств, то обычно в запасе необходимо иметь хотя бы одну значащую цифру. Подбор эмпирической формулы по экспериментальным данным Во многих экспериментах преобразование данных не позволяет получить линейный график и необходимо подбирать более общие функции, например: Y = a + bX + cX2 + dX3+…+nXm. (1) Еслииспользуем только 2 первых члена, то имеем общее уравнение прямой, если 3 – то имеем параболу, проверку которой проводят по данным таблицам (см. «Способы построения линейных графиков»). Увеличивая число членов уравнения получаем более сложные кривые. При подборе уравнения типа (1) на кривой выбирается столько точек, сколько постоянных должно быть определено, а затем решается система (п+1) уравнений. К сожалению прип =2 и более такой способ становится громоздким. Трудности возникают при решении с помощью определителей.
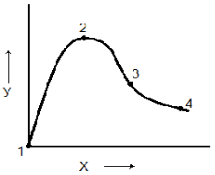
Допустим, что для кривой (см. рис.17) необходимо подобрать уравнение при п = 3. Левая часть кривой с непрерывно убывающим наклоном представляет собой функцию простого вида, а правая имеет точку перегиба. Т.о. можно предположить, что подобрать уравнение для правой части кривой труднее, поэтому возьмем больше точек на этом участке. После того, как будет найдено уравнение для п = 3, надо проверить остальные точки, чтобы убедиться в том, что получено удовлетворительное соответствие для всей кривой.
Рис.17. Кривая для подбора уравнения Если получено недостаточно хорошее соответствие, то подбираем 4 другие точки или перейти к уравнению для п = 4. Если кривая проходит через начало координат, то постоянная а в формуле (1) равна нулю и система будет иметь на одно уравнение меньше (либо порядок определителей будет на единицу меньше).Такой результат получается переносом координат (см. рис.18). В системе координат (Х 1, Y 1) имеем: Х1=Х –Δх; Y1 =У – Δу Если имеем многочлен 2ой степени Y = a + bX = cX2,(2) то уравнение имеет вид: Y- Δу = a1+b1(X-Δx)+c1(X-Δx)2. (3) Рис.18. Пример переноса координат После определения b1 и c1 и учитывая, что постоянная а в системе координат ( Х 1, Y 1 ) равна 0, можно соотношение (3) преобразовать и вернуться к первоначальной системе координат: Y = Δу – b1Δx + c1(X 2- 2XΔx) или: Y = Δу – b1Δx + c1Δx2 + X(b1 - 2Δx) + c1X 2. Такие преобразования всегда удобны, но многочлен, имеющий более 3х постоянных, трудно подобрать при вычислении в ручную.
Пример: Имеем зависимость анодного тока от анодного напряжения в триоде при постоянном напряжении на сетке, равном 5в (зависимость в форме кривой представлена на рис.19. Найти: Уравнение этой кривой.
Переносим начало координат в точку (20;0). Получаем V 1 = V-20 и I 1 = I. В этом случае a1 = 0.Тогда 11 = b1(V-20)+ c1(V-20) (cм. формулу (2)). На кривой можно выбрать 2 точки с одинаковыми приращениями координаты У. Однако, понимая, что в нижней части кривая имеет большую кривизну и здесь труднее подобрать уравнение. Выбрав 2 точки (V = 90 и 1= 50) и (V = 170 и 1= 200), найдем b1 и c1.
Рис.19. Зависимость анодного тока от анодного напряжения в триоде
Получаем уравнения: 50 = b1 · 70 + c1 · 70 2; 200 = b1 · 150 + c1 · 150 2 Решая уравнения, получаем: b1=0,171; c1 = 0,007. Далее: I = 0,171(V-20) – 0,007(V 2- 40V+400), Следовательно уравнение данной кривой имеет вид: I = 0,007V 2 – 0,137V –0,33. Для проверки соответствия полученного уравнения находятся значения I при различных значениях V. Полученные значения нанесены на график при V = 40, 80, 120, 160в. Предсказанная величина I на 1та больше на нижнем конце кривой и на 2 та меньше на верхнем. Эта ошибка не превышает 2%. Ошибку можно уменьшить, подобрав кубическое уравнение Y = a + bX + cX 2 + dX 3.
Интерполяция и экстраполяция Интерполяция – вычисление величины, которая находится между 2мя известными величинами с использованием коэффициентов. Экстраполяция – распространение выборочных данных на другую ее часть. Если точки на плоскости Х,У образуют плавную кривую, то графики можно использовать для интерполяции данных с большой точностью Интерполяция особенно важна при проведении факторного * эксперимента, когда невозможно определить необходимые промежуточные значения. * Однофакторный – одна независимая (или регулируемая) переменная Х и зависимая У. Многофакторный – две или более регулируемые переменные Допустим, что при проведении эксперимента получены точки (Х1 , У1), (Х2 , У2),…, (Хп , Уп). Требуется: найти У при значении Х (не установленное). Применим интерполяционную формулу Лагранжа, которая для нашего случая имеет вид:
Пример:При испытаниях ДВС получены следующие данные:
Предположим: сомнение по данным при F = 44кг. Вопрос: Какой расход горючего может предсказать формула Лагранжа? Решение: Отсчет в эксперименте равен 11,9. Если нанести указанные 3 точки на график и провести через них плавную кривую, то получим значение, лежащее в интервале от 11,4 до 11,5. Преимущество математического метода состоит в том, что он может применяться автоматически и в последствие его можно продублировать каким-либо другим методом для получения точного интерполированного значения Формула Лагранжа дает приемлемую точность, если берется не слишком большой интервал экстраполяции. Этот метод предпочтительнее графической экстраполяции осуществляемой на глаз. Методы экстраполяции во многих случаях сходны с методами интерполяции. Дифференцирование и интегрирование
|

 Не зависимо от того, какой способ решения системы уравнений выбран (непосредственно или с помощью определителей), необходимо выбрать 2 –3 или большее число точек, чтобы подобрать наилучшую функцию.
Не зависимо от того, какой способ решения системы уравнений выбран (непосредственно или с помощью определителей), необходимо выбрать 2 –3 или большее число точек, чтобы подобрать наилучшую функцию.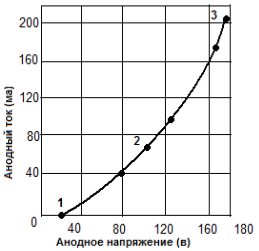 Решение: На кривой отсутствуют максимумы или явные перегибы. В этом случае кривой может соответствовать многочлен 2го порядка.
Решение: На кривой отсутствуют максимумы или явные перегибы. В этом случае кривой может соответствовать многочлен 2го порядка.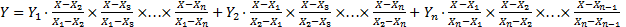 (4)
(4)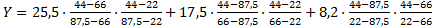 = 11,66
= 11,66


