Отклоняющиеся точки следует исключать, пользуясь статистическим критерием, и только в том случае, если они находятся в средней части графика.
Основные критерии, на основе которых должны исключаться данные, имеют как физическую, так и статистическую природу: 1. Явно неудовлетворительный контроль (резкое увеличение U в сети). 2. Явная неисправность прибора (если несколько точек резко отклоняются и, кроме того, распределены случайным образом — имеет место при рандомизированном плане — то можно ожидать, что измерения выполнены неправильно - исключить). 3. Нарушение баланса сверх установленного предела (при условии, что для каждой точки можно использовать уравнение баланса). 4. Нарушение статистического критерия. Существует несколько статистических критериев. Критерий Шовене. Допустим, что рассматриваемые ошибки распределены по нормальному закону, поэтому можно использовать для нахождения вероятностей таблицы зависимости Pηx = f(ηx),где Pηx — вероятность, что данное отклонение лежит в интервале от + ηx до - ηx (η — постоянная, характеризующая нормальное распределение — модуль или показатель точности). Согласно указанному правилу какой либо отсчет из ряда п отсчетов следует исключить в том случае, когда величина его отклонения от истинного или среднего значения такова, что вероятность появления этого отклонения не превышает Пример: Пусть мощность имеющегося двигателя вычислена с вероятностью ±0,05 квт. Было получено 8 значений мощности и одно из них отклоняется от среднего значения на 0,12 квт. Вопрос: следует ли резко отклоняющееся значение исключить? Решение: Зная вероятную ошибку, найдем сначала η;. Из формулы Ф = Вероятность по Шовене Рш = Далее определяем, будет ли при η = 9,55 квт-1 и нормальном распределении вероятность того, что отклонение превысит 0,12 квт (больше ил меньше 6,25%). В нашем случае ηх = 9,55 ∙ 0,12 = 1,14. Вероятность того, что какой-либо отсчет превысит это значение ηх равно: Pηx = 1 - 0,893 =0,107 или 10,7%. Применяя критерий Шовене видим, что с вероятностью 10,7% отклонения превышают ± 0,12 квт. Эта вероятность больше, чем 6,25%, поэтому данный результат не следует исключать. Какие отклонения следует отбрасывать, используя критерий Шовене? Любое отклонение не попадающее в вероятностный диапазон 1 - 0,0625 = 0,9375 = Pηx ( если п = 8 ). Из таблицы зависимости Pηx = f(ηx) находим, что ηx = 1,31. Откуда хш =
|

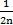
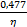 =0,05квт имеем η; =
=0,05квт имеем η; =  = 9,55квт-1.
= 9,55квт-1. = 0,0625 (6,25%).
= 0,0625 (6,25%). = 0,138 квт. Итак: 0,12квт < 0,138квт — отбрасывать нельзя.
= 0,138 квт. Итак: 0,12квт < 0,138квт — отбрасывать нельзя.


