В математическом описании обязательно используются операция измерения физической величины, т.е. сопряжения ее с числом.
Рис.3. Распределение отклонений отсчетов Oдно из основных положений теории вероятности: Вероятность появления всей выборки, состоящей из n отсчетов равно произведению вероятностей появления отдельных отсчетов. ∆; P = ∆P1 · ∆P2 ·…·∆Pn
Сумма квадратов отклонений от наилучшего или точного отсчета должна быть минимальной. Дифференцируя ∆Рсум по xс получим:
Эта производная равна нулю в одном случае - когда Пример: Оптический пирометр установлен на светящуюся нить накала. Операторами произведено несколько измерений t0c
Предположение: выборка взята из нормально распределенной совокупности Найти: среднеквадратическое отклонение S и вероятную ошибку Ф Решение: Находим среднее значение хс : Запишем данные в более удобном для вычислений виде
Cведем значения отклонений x и их производных в таблицу:
∑ n = 46; ∑ x2 = 43125;
Ошибки и неопределенности эксперимента в целом. Показатель точности произведения или частного. Рассмотрим результат R, как линейную функцию произведения двух измеряемых величин X и Y: R = kX·Y, где k - нормирующий множитель, точно известный. Для X выборочное среднеквадратическое число равно Sx,а для Y – Sy; х1 – данное отклонение от точного значения Хс, обусловленное наличием случайной ошибки при измерении Х, а y1 – одновременно наблюдаемое отклонение от точного значения Yс. Формула для пары отсчетов, взятой из выборки, содержащей n таких пар, имеет вид: Rc + r1 = k (Хc + x1) · (Yc + y1), (17) где r1 – отклонение результата. или Rc + r1 = k (XcYc + x1 Yc + Xc y1 + x1y1) Произведением x1 y1 можно пренебречь ввиду малых величин. Тогда r1 = (x1Yc + y1Xc), аналогично для другой пары: r2 = (x2Yc + y2 Xc) и т.д. Из определения среднеквадратического отклонения имеем Просуммировав n аналогичных уравнений получим: ∑; r2 = k2[ Y2c ∑x2 + Xc Yc ∑(x y) +X2c ∑y2] (19) ∑(x y) можно полагать равной нулю, т.к. любое произведение x и y может быть с равной вероятностью как положительным, так и отрицательным, а для большой выборки сумма этих произведений будет стремиться к нулю. Подставляя ∑r2 в формулу вычисления S2r (18) получим:
Подставляя в формулу S, полученную ранее, выражение R = k XY после преобразований имеем:
Формула (20) справедлива для случаев Причем Для случая произвольного интервала отклонений
Доверительный интервал.
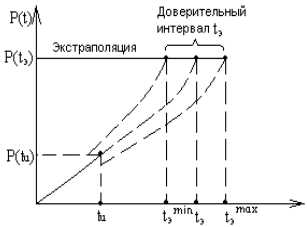
Коэффициент ускорения испытаний:
где tи - длительность ускоренных испытаний.
Рис.4. График, характеризующий ускоренные испытания.
Определение показателей точности для произвольной функции. Результат R является функцией двух измеряемых переменных X и Y: Rс + r1 = f (Хc+x1;Yc+y1). Теорема Тейлора: Если функция y = f (x) в интервале [ a, a+h ] непрерывна и имеет непрерывные производные от 1ой до nой включительно, то имеет место равенство:
Рассмотрим только два члена ряда, тогда:
или поскольку Rс = f (Хc;Yс): где x и y в индексах обозначают отклонения от точных отсчетов.
∑x y стремится к нулю, Интервал неопределенности ω; получаем из выражения
± ω- произвольный интервал отклонений – интервал, в котором могут находиться 50, 68, 95% всех отсчетов данного прибора. Применение общего уравнения. Уравнения (23) и (24) играют важную роль. Рассмотрим их применение на примерах:
1. Дано: Функция R = k X b, где k и b – постоянные. Найти: Среднеквадратическое отклонение результата R при заданном среднеквадратическом отклонении Sx измеряемой переменной Х. Решение: Из уравнения (24) находим dR / dX = b k X b-1 и S2r = b2 k2 X 2(b-1) S2x Разделив выражение S2r на R = k X b, возведенное в квадрат, получим: 2. Дано: Функция Найти: Вероятную ошибку для R Решение: Имеем: Тогда по формуле (24) полагая, что ω = Ф, получим: Для нахождения относительной ошибки делим наR2:
Примеры: 1. Дано: Момент асинхронного электродвигателя пропорционален напряжению U2(в квадрате). Найти: Какой будет ошибка при определении момента М, если среднеквадратическое отклонение S u напряжения составляет 2,5%. Решение:M =kU2 (формула в общем виде R = k X b);
Проведя сокращения, получаем: Ошибка в определении момента будет равна 5% 2. Дано: Функция R1=75 ом с вероятностью ошибки ±5%, R2=100ом с вероятной ошибкой ±3%. Найти: Вероятную ошибку для R, Решение: В нашем случае: Вычисляя получаем
Некоторые формулы для определения ошибки результата.
Анализ ошибок при планировании экспериментов. При проведении эксперимента изучение ошибки результата позволяет: - предсказать ошибки для системы в целом; - обнаружить “слабые” места в выполняемых измерениях; - выбрать правильный план проведения эксперимента. Нахождение неопределенности результата с помощью графиков и диаграмм. Пример: Отсчет х прибора имеет неопределенность ωх. Для получения результата R необходимо воспользоваться графиком зависимости R от х.
Из уравнения интервала неопределенности:
Если значение
Рис.5. Определение угла наклона кривой графика. Уменьшение набора переменных. Анализ размерностей. Цель такого планирования – получение максимального объема полезных данных при наилучшем контроле и минимальных затратах времени на их обработку.. Самый известный и эффективный) способ – анализ размерностей – метод сокращающий объем многих экспериментов без потери контроля. Применяется как способ объединения нескольких переменных в одну; Теорема Букингема. Для правильного анализа размерностей необходимо знать характер и число фундаментальных переменных в эксперименте. Фундаментальная переменная – величина, оказывающая влияние на эксперимент и способная изменяться независимо от других переменных. Первая часть теоремы Букингема: Если уравнение однородно относительно размерностей, то оно может быть представлено в безразмерном виде. Однородным относительно размерностей является уравнение, форма которого не зависит от выбранных основных единиц. Пример:R = f(U,I). Возможно записать в форме: где k – безразмерный коэффициент, равный 1 при U (вольт), I (ампер), R (ом), но изменяющейся, если какая либо величина имеет другую размерность (к ом,к вольт). При анализе размерностей соотношений, характеризующих эксперимент, необходимо помнить постулаты: 1 - Любое явление или процесс, подчиняющийся действию физических законов, должны иметь математическое описание. В математическом описании обязательно используются операция измерения физической величины, т.е. сопряжения ее с числом. • Первичные величины х измеряются путем прямого сопоставления их с эталонами х0: Пример: выбрав за эталон х0 =1см можно выразить (записать) размеры тетради X1=28, X2=20. Если х/0 = 1дм, то получим X1 = 2,8; X2 = 2,0. Т.о. сами числовые значения нельзя считать абсолютными признаками какого-либо объекта – они по своей сути относительны. Абсолютный признак – отношение численных значений:
Это важное свойство в анализе размерностей называется абсолютностью отношений. Оно отражает первый постулат и для первичных величин выполняется автоматически • Вторичные величины yвыражаются через первичные посредством определительного уравнения y = f(xi). Ихчисленное значение y зависит как от эталонов х0 , так и от вида управления (в рассмотренном ранее случае R = U / I ). В соответствии с первым постулатом должна существовать абсолютность отношений, т.е. если Выполнение этого условия возможно лишь при следующем виде определительного уравнения: тогда где a1, ai и am - показатели размерности. Тогда (с учетом Полученный результат можно распространить на случай, когда вторичная величина не зависит от «m» первичных и «r» вторичных, т.е. y = f(x1… xm, y1… yr), тогда
Формулы Пример: Скорость V - вторичная величина, выражается через первичные: путь х1 = S и время x2 = t Определительное уравнение Тогда формула размерности: kv = ks k-1t. Можно также · Размерность первичной величины совпадает с ее символом · Безразмерные величины имеют «нулевые» показатели размерности. Условие однородности уравнения означает отличие от нуля всех входящих в него показателей степени. Невыполнение этого условия показывает, что исходная запись некорректна и в ней не соблюдены физические законы, либо пропущены существенные для данной задачи параметры и константы, либо, напротив, присутствуют величины, не влияющие на изучаемый процесс, т.е. не существенные для данной задачи. Однородность уравнения не гарантирует правильности постановки задачи. Она лишь свидетельствует о том, что противоречия с физическими законами не содержится. Вторая часть теоремы Букингема (π- теорема). Если существует соотношение f (A1…An) = 0 между «n» физическими величинами, для описания которых используется «k» основных единиц, то существует также соотношение f′;(π1…πn-k) = 0 между n –kбезразмерными комбинациями, составленными из этих физических величин. или: Число безразмерных комбинаций равно числу переменных, параметров и констант,
|

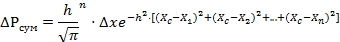
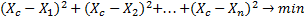
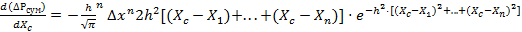


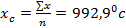


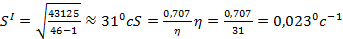
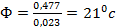 В итоге: 993 ± 210с
В итоге: 993 ± 210с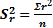 (18)
(18)
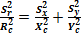 (20)
(20)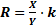 и
и 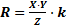 ; в последнем случае используется выражение
; в последнем случае используется выражение 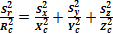 (21)
(21)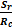 есть отношение среднего квадратического отклонения к точному отсчету и, следовательно, является показателем точности, выражаемом в %.
есть отношение среднего квадратического отклонения к точному отсчету и, следовательно, является показателем точности, выражаемом в %. формула имеет вид:
формула имеет вид: (22)
(22)
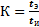
 - доверительная граница интервала значений Ky
- доверительная граница интервала значений Ky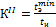 - доверительная граница интервала значений Ky
- доверительная граница интервала значений Ky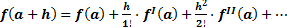 т.е. можно рассматривать как сумму степенного ряда.
т.е. можно рассматривать как сумму степенного ряда.
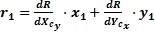
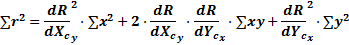
 и поэтому:
и поэтому: 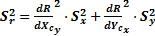 (23)
(23)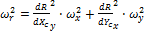 (24)
(24)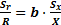
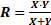
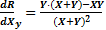 и
и 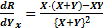
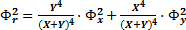
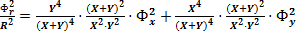 Выполнив преобразования получим:
Выполнив преобразования получим: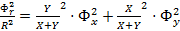
 (формула в общем виде:
(формула в общем виде: 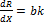 ∙ X b-1);
∙ X b-1); 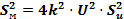 (формула в общем виде: S2r = b2 k2 X 2(b-1) S2x);
(формула в общем виде: S2r = b2 k2 X 2(b-1) S2x);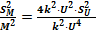 (формула в общем виде:
(формула в общем виде: 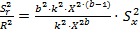 )
)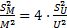 или
или 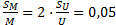

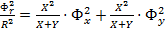 - общее уравнение.
- общее уравнение.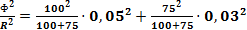
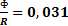 или 3,1%; R = 42,9oм, тогда 3,1% составляет 1,33Ом.
или 3,1%; R = 42,9oм, тогда 3,1% составляет 1,33Ом.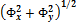
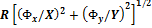
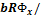 X
X

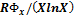
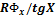
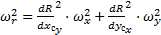 следует
следует  (для данного случая)
(для данного случая)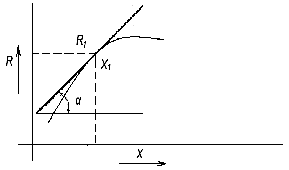 Один из способов нахождения производной функции R = f(x) в точке (R1 x1) для использования в формуле определения ошибки результата: на графике (рис.5) проводим касательную в указанной точке, определяем тангенс угла наклона
Один из способов нахождения производной функции R = f(x) в точке (R1 x1) для использования в формуле определения ошибки результата: на графике (рис.5) проводим касательную в указанной точке, определяем тангенс угла наклона 
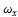 может быть оценено, то применение формулы
может быть оценено, то применение формулы 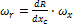 не вызывает затруднений.
не вызывает затруднений.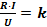 ;
;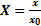 где X – численное значение величины х при эталоне. x0 .
где X – численное значение величины х при эталоне. x0 .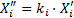 , где
, где 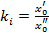
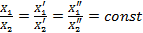 , не зависящее от выбранных эталонов х0.
, не зависящее от выбранных эталонов х0.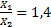 - признак объекта (тетради), инвариантный к выбранной системе единиц (эталонов длины).
- признак объекта (тетради), инвариантный к выбранной системе единиц (эталонов длины). ,
, 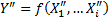 , то
, то  . (
. (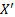 – вольт,
– вольт, 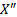 - киловольт)
- киловольт)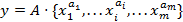 ,
,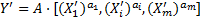 и
и 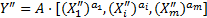 ,
,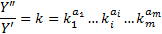
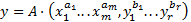 и
и 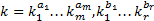 .
. и
и 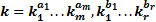 естьформулы размерности, а показатели степени в них – показатели размерности.
естьформулы размерности, а показатели степени в них – показатели размерности.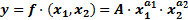 , где А =1, a1 = 1, a2 = -1
, где А =1, a1 = 1, a2 = -1 , где L и T - символы длины и времени, [V] – размерность скорости, выраженная через первичные величины.
, где L и T - символы длины и времени, [V] – размерность скорости, выраженная через первичные величины.


