Розв’язання. Рядом динаміки або динамічним рядом називають ряд розміщених у хронологічній послідовності числових даних (статистичних показників)
Рядом динаміки або динамічним рядом називають ряд розміщених у хронологічній послідовності числових даних (статистичних показників), які характеризують величину суспільного явища на даний момент або за певний період часу. Ряди динаміки складаються з двох елементів: рівнів ряду yi (i = 1…n) та часу ti. Для оцінювання властивостей динаміки у статистиці застосовуються взаємопов’язані характеристики або аналітичні показники. Визначимо ланцюгові і базисні показники динаміки, а саме: - абсолютний приріс; - темп зростання; - темп приросту; - абсолютне значення одного відсотку приросту.
Абсолютний приріст (або зменшення) - базисний - ланцюговий де y0 – базовий рівень ряду динаміки (за умовою задачі – це 1998 рік); n – кількість рівнів ряду динаміки (за умовою задачі 6 років).
Абсолютні прирости податкових надходжень ланцюгові, млрд. грн.:
Абсолютні прирости податкових надходжень базисні, млрд. грн.:
Ланцюгові та базисні абсолютні прирости пов’язані між собою залежністю (сума ланцюгових приростів дорівнює кінцевому базисному):
Темп зростання Ki характеризує інтенсивність змін рівнів ряду і виражається у відносних величинах числом або у процентах: - базисний - ланцюговий Отже, темп зростання податкових надходжень ланцюговий дорівнює:
Темп зростання податкових надходжень базисний дорівнює:
Добуток ланцюгових темпів зростання дорівнює кінцевому базисному:
Темп приросту Ті виражається у процентах і показує на скільки рівень уі більший (менший) від рівня, взятого за базу порівняння: базисний ланцюговий
Між темпом приросту і темпом зростання існує такий зв’язок:
Темп приросту податкових надходжень ланцюговий дорівнює: Т1999/1998=115,14-100=15,14% Т2000/1999=124,70-100=24,70% Т2001/2000=117,25-100=17,25% Т2002/2001=123,71-100=23,71% Т2003/2002=119,60-100=19,60%
Темп приросту податкових надходжень базисний дорівнює: Т1999/1998=115,14-100=15,14% Т2000/1998=143,58-100=43,58% Т2001/1998=168,35-100=68,35% Т2002/1998=208,26-100=108,26% Т2003/1998=249,08-100=149,08%
Абсолютне значення одного проценту приросту Аі характеризує вагомість кожного проценту приросту і розраховується як відношення абсолютного приросту до темпу приросту:
Розрахунок цього показника має економічний зміст тільки на ланцюговій основі, оскільки на базисній основі для всіх рівнів буде отримано те саме значення показника – сота частина базисного (першого) рівня. Цей показник має важливе практичне значення в економічному аналізі; так в динамічних рядах, що постійно зростають, темпи зростання можуть сповільнюватись, або залишатися на одному рівні, а значення одного проценту приросту зростати.
Для узагальнюючих характеристик ряду динаміки явища розрахуємо також середні показники: - середні рівні динамічного ряду; - середні з аналітичних показників. Ряд динаміки податкових надходжень є прикладом інтервального ряду, тобто такого ряду, рівні якого характеризують явище за певний період часу. Рівні інтервальних рядів дають підсумкові, результативні показники, які відповідають інтервалу часу, тому їх можна підсумувати та ділити. При підсумуванні рівнів ряду знаходять накопичені підсумки. Оскільки ряд динаміки податкових надходжень є інтервальним, то середній рівень податкових надходжень розраховується за формулою середньої арифметичної простої:
Середній абсолютний приріст податкових надходжень визначається за наступною формулою:
Середній темп зростання за період з 1998 по 2003 роки розраховується за формулою:
Середній темп приросту за досліджуваний період обчислюється за формулою:
Результати розрахунків темпів зростання занесемо у таблицю.
Аналітичні показники динаміки податкових надходжень дозволяють зробити наступні висновки: - у 2003 році податкові надходження у порівнянні з 1998 роком збільшились на 32,5 млрд. грн. або в 2,4908 рази (на 149,08%), а порівняно з 2002 роком – на 8,9 млрд. грн. або в 1,196 рази (на 19,6%). Кожний відсоток абсолютного приросту у 2003 році становив 0,454 млрд. грн. Таким чином, динаміка податкових надходжень є позитивною, а показники податкових надходжень зростають із року в рік; - середній рівень податкових надходжень в період з 1998 по 2003 роки складає 35,767 млрд. грн.. При цьому середній абсолютний приріст податкових надходжень за 1998-2003 роки дорівнює 6,5 млрд. грн. Податкові надходження за період, що аналізується, щорічно зростали в 1,2002 рази, або на 20,02%.
ЗАДАЧА 5. Визначення показників швидкості обороту оборотних засобів,
|

 відповідає швидкості зміни рівнів ряду і розраховується як різниця рівнів ряду:
відповідає швидкості зміни рівнів ряду і розраховується як різниця рівнів ряду: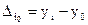
 , i = 1…n,
, i = 1…n,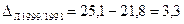

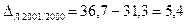
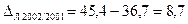

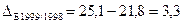
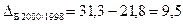
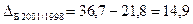
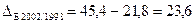
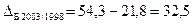
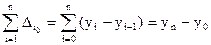 .
.
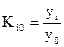 ;
; .
.



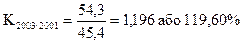
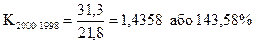
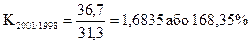


 .
.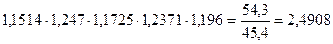
 ;
;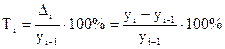 .
.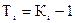 або
або 
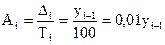 %.
%.
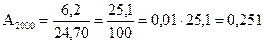
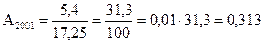
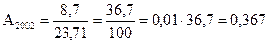
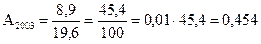
 .
. млрд. грн.
млрд. грн. або
або 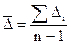
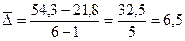 млрд. грн. або
млрд. грн. або 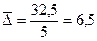 млрд. грн.
млрд. грн.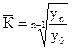 .
.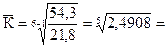 1,2002 або 120,02%.
1,2002 або 120,02%.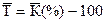 .
.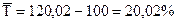 .
.



