Алгоритм Мамдани
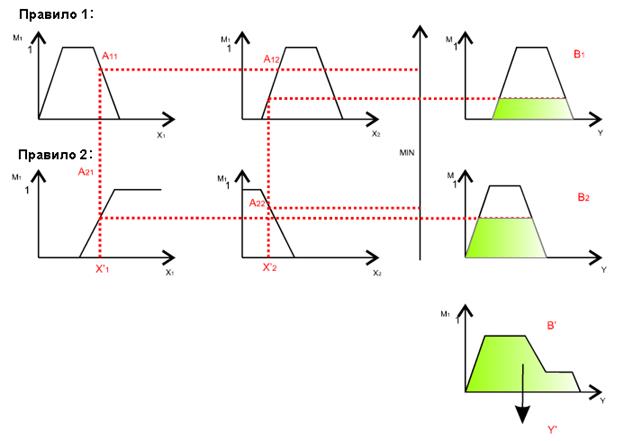
Алгоритм Мамдани предложен одним из первых для управления паровым двигателем и описывается следующим образом. r Формирование базы правил систем нечеткого вывода и введение нечеткости для входных переменных. Предположим, что база состоит из двух правил (см. рис. 2.11) с двумя входами и одним выходом: Правило 1: ЕСЛИ x1 есть А11 И x2 есть А12 ТО y есть B1, Правило 2: ЕСЛИ x1 есть А21 И x2 есть А22 ТО y есть B2. r Агрегирование подусловий в нечетких правилах продукций. Для нахождения степени истинности условий каждого из правил нечетких продукций используются парные нечеткие логические операции. Правила, степень истинности условий которых отлична от нуля, считаются активными. r Активизация подзаключений в нечетких правилах продукций выполняется с помощью min - активизации по формуле (2.5): m¢(y) = min{ ci, m(y)}; причем, для сокращения времени вывода учитываются только активные правила. r Аккумулирование заключений нечетких правил продукций выполняется с помощью max-объединения по формуле (1.4) для объединения нечетких множеств, соответствующих термам подзаключений, относящихся к одним и тем же выходным лингвистическим переменным. r Дефаззификация выходных переменных выполняется с использованием метода центра тяжести (2.11)—(2.12) или метод центра площади (2.13).
Рис. 2.11. Представление алгоритма Мамдани
|