TE моды
Для рассматриваемой геометрии планарного волновода TE -моды характеризуются условием: Ez =0. Исходя из рассмотрения системы уравнений (16), получаем Ex = Hy =0, т.к. ∂Hz / ∂y =0. Поэтому единственными компонентами поля в этом случае являются Hx, Ey и Hz. Тогда
где k 2= k 02 n (x)2. Компоненты Hx и Hz могут быть определены из Ey, используя соотношения (15), (16):
рис.11. Геометрия пластины с показателем преломления n 1 между двумя диэлектриками с показателем преломления n 2.
В случае TM -моды планарного волновода, TM =0. Тогда Hx = Ey =0, т.к. ∂Ez / ∂y =0. В этом случае светового поля будут Ex, Hy и Ez. Волновое уравнение в этом случае имеет вид:
где k 2= k 02 n (x)2.
В качестве первого примера рассмотрим световое поле в пластине с показателем преломления n 1 между двумя слоями диэлектрика с одинаковым показателем преломления n 2 (рис.11). В этом случае уравнения (18) и (20) имеют один и тот же вид. Обозначим как q =
Для нахождения неизвестных коэффициентов A, B, C и D используем условия равенства рассматриваемых функций на границах раздела и условие симметрии задачи. Когда распределение показателя преломления вдоль оси x симметрично, то решениями волнового уравнения будут либо симметричные, либо антисимметричные моды по отношению к плоскости симметрии планарного волновода (y - z плоскости при x =0). Тогда
Комбинируя (22), (23) и (21), имеем:
где Тогда, учитывая, что q =
Это означает, что значения ρ; и ν; лежат на окружности радиуса V, который равен
рис.12. Графическое рассмотрение распространение света в планарном волноводе. Величина V известна как безразмерный параметр светового волновода и, если он задан, то значения ρ; и ν; определяются из (27) и (23), (24). Это удобно делать графическим методом, как это показано на рис.12. При уменьшении световой частоты ω; с одновременным уменьшением ρ; к началу координат, все пересечения графиков исчезают за исключением одного пересечения с ветвью тангенса. Это соответствует фундаментальной моде m =0 без отсечки частоты. Т.е. такая мода с распределением напряженности TE -волны, как это показано в правой части рис.13 имеет право на распространение. И геометрическая интерпретация в основном относиться именно к этой ситуации. Все высшие моды с m >0 имеют отсечку. Они не могут распространяться в волноводе выше определенной частоты отсечки. Два круга на рис.12 соответствуют значениям V /2=2 и V /2=5; при этом число разрешенных мод может быть показано в следующей таблице:
рис.13. Характер распространения симметричной и антисимметричной TE 1 световой волны в планарном волноводе. Характер полевой структуры (распределение напряженностей электрического и магнитных полей по сечению планарного волновода) симметричной и антисимметричной TE волны показан на рис.13. Если в случае симметричной структуры напряженность TE волны принимает максимальное значение в начале координат, то в антисимметричном случае напряженность поля равна нулю. Для TH волны имеет место симметричный и обратный случай.
|

 , (18)
, (18) ,
, 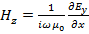 . (19)
. (19)
 , (20)
, (20)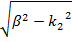 и h = k 1cos(θ;)=
и h = k 1cos(θ;)=  . Решения уравнения (18) для разных областей в этом случае будет иметь вид:
. Решения уравнения (18) для разных областей в этом случае будет иметь вид: . (21)
. (21) - симметричная мода, (22)
- симметричная мода, (22) - антисимметричная мода. (23)
- антисимметричная мода. (23) - симметричная мода, (24)
- симметричная мода, (24) - антисимметричная мода, (25)
- антисимметричная мода, (25) и
и  .
. . (26)
. (26) . (27)
. (27)




