ПОСТРОЕНИЕ КРИВЫХ

Важное значение при формировании как 2D, так и 3D моделей имеет построение элементарных кривых. Кривые строятся в основном следующими способами:

Ø той или иной интерполяцией по точкам;

Ø вычислением конических сечений;

Ø расчетом пересечения поверхностей;

Ø выполнением преобразования некоторой кривой;

Ø формированием замкнутых или разомкнутых контуров из отдельных сегментов, например отрезков прямых, дуг конических сечений или произвольных кривых.

В качестве последних обычно используются параметрические кубические кривые, так как это наименьшая степень, при которой обеспечиваются:

Ø непрерывность значения первой (второй) производной в точках сшивки сегментов кривых;

Ø возможность задания неплоских кривых.

Параметрическое представление кривых выбирается по целому ряду причин, в том числе потому, что зачастую объекты могут иметь вертикальные касательные. При этом аппроксимация кривой y = f(x) аналитическими функциями была бы невозможной. Кроме того, кривые, которые надо представлять, могут быть неплоскими и незамкнутыми. Наконец, параметрическое представление обеспечивает независимость представления от выбора системы координат и соответствует процессу их отображения на устройствах: позиция естественным образом определяется как две функции времени x(t) и y(t).

В общем виде параметрические кубические кривые можно представить в форме:

x(t) =   A11 t3   +   A12 t2   +   A13 t   +   A14;   y(t) =   A21 t3   +   A22 t2   +   A23 t   +   A24;   z(t) =   A31 t3   +   A32 t2   +   A33 t   +   A34,

где параметр t можно считать изменяющимся в диапазоне от 0 до 1, так как интересуют конечные отрезки.

Существует много методов описания параметрических кубических кривых. К наиболее применяемым относятся:

Ø метод Безье, широко используемый в интерактивных приложениях; в нем задаются положения конечных точек кривой, а значения первой производной задаются неявно с помощью двух других точек, обычно не лежащих на кривой;

Ø метод В-сплайнов, при котором конечные точки не лежат на кривой и на концах сегментов обеспечивается непрерывность первой и второй производных.

В форме Безье кривая в общем случае задается в виде полинома Бернштейна

P(t) = ,

где P_i - значения координат в вершинах ломаной, используемой в качестве управляющей ломаной для кривой; t - параметр;

 

Cmi = m! i! (m-i)! .

При этом крайние точки управляющей ломаной и кривой совпадают, а наклоны первого и последнего звеньев ломаной совпадают с наклоном кривой в соответствующих точках.

Предложены различные быстрые схемы для вычисления кривой Безье.

В более общей форме B-сплайнов кривая в общем случае задается соотношением

P(t)= ,

где P_i - значения координат в вершинах ломаной, используемой в качестве управляющей ломаной для кривой; t - параметр; N_im - весовые функции, определяемые рекуррентным соотношением:

 

Ni,k(t) = (t - xi) Ni,k-1(t) xi+k-1 - xi + (xi+k - t) Ni+1,k-1(t) xi+k - xi+1 .

Используются и многие другие методы, например метод Эрмита, при котором задаются положения конечных точек кривой и значения первой производной в них.

Общее в упомянутых подходах состоит в том, что искомая кривая строится с использованием набора управляющих точек.
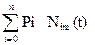