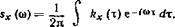По теореме о среднем,
&*= (<*ь—<*«) (“*) = (юе), где юа < < со6. Отсюда (®с) = DJ Дсо. Из этой формулы заключаем: а) величину sx (со,.) можно истолковать как среднюю плотность дисперсии на частичном интервале Дю, содержащем частоту о>с; б) при Д<о —>- 0 естественно считать, что sx (сос) — плотность дисперсии в точке сое. Поскольку никаких ограничений на частоту наложено не было, полученный результат справедлив для любой частоты. Итак, спектральная плотность описывает распределение дисперсий стационарной случайной функции по непрерывно изменяющейся частоте. Из вероятностного смысла спектральной функции следует, что спектральная плотность — неотрицательная фуНКЦИЯ Пример 1. Найти спектральную плотность стационарной случайной функции X (/), зная ее корреляционную функцию Интегрируя по частям, окончательно получим искомую спектральную плотность: sx (ш) = sin2 <о/(пи>2). Пример 2. Найти спектральную плотность стационарной случайной функции X (/), зная ее корреляционную функцию kx (т) = De~“ 1 *1, а > 0. Решение. Используем формулу Оо
— 00 Учитывая, что |т| = — т при т < 0, |т|=т при тг^гО, получим kx(i)=Deax при т < 0, kx(x ) = De~“x при тЭ=0. Следовательно, Пример 3. Найти корреляционную функцию стационарной случайной функции X (t), зная ее спектральную плотность { s0 в интервале —
|