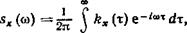Среди стационарных случайных функций есть такие функции, корреляционные функции которых нельзя представить в виде
kx (т) = 2 A cos №/т (А > °)i где число слагаемых конечно или счетно. Спектр этих функций не дискретный, а непрерывный. Для рассмотрения стационарных случайных функций с непрерывным спектром необходимо ввести понятие спектральной плотности. Выше, когда частоты гармоник спектрального разложения стационарной случайной функции были дискретными и равноотстоящими, был получен дискретный линейчатый спектр, причем соседние частоты отличались на величину Д(о = п /Т. Пусть Т —►оо, тогда До»—*-0. Ясно, что при этом частота изменяется непрерывно (поэтому обозначим ее через со без индекса), соседние ординаты спектра сближаются и в пределе вместо дискретного спектра мы получим непрерывный спектр, т. е. каждой частоте <о (о) ^ 0) соответствует ордината, которую обозначим через sx (со). Хотя отрицательные частоты физического смысла не имеют, для упрощения вычислений целесообразно считать, что частоты изменяются в интервале (—оо, оо), и вместо функции sj(co) рассматривать функцию, которая имеет вдвое меньшие ординаты: s*((d) = s*((d)/2. Спектральной плотностью стационарной случайной функции X (/) называют функцию ях((о), которая связана с корреляционной функцией kx(r) взаимно обратными преобразованиями Фурье:
— 00 Ое **(*) = S sx(v>)tl<atdo>;. Ао Эти формулы называют формулами Винера — Хинчина. В действительной форме они представляют собой взаимно обратные косинус-преобразования Фурье: Важное значение спектральной плотности состоит в том, что, зная ее, можно найти корреляционную функцию, и обратно (в этом смысле спектральная плотность и корреляционная функция эквивалентны); кроме того, как уже было указано, использование спектральной плотности в ряде случаев значительно упрощает теоретические и практические расчеты. Подчеркнем, что, как следует из формулы (***), спектральная плотность—четная функция: «*(—(й) = 5* (ш). Выясним вероятностный смысл функции sx(co). Положив т = Ов соотношении (****•) и учитывая, что kx(0)~Dx, sx(<a )— четная функция, получим Со оо Dx = 2 J sx (to) dio = ^ sx(co)d©. О — оо Видим, что дисперсия стационарной случайной функции X ( t ) представляет собой «сумму» элементарных дисперсий sx (ю) d(D = sx (to) Aw; каждая элементарная дисперсия соответствует частичному интервалу частот Дм. В частности, частичному интервалу Дю —<ой—<оЛ соответствует дисперсия А*= $ sx(ca)d&;. аа
|