Модели следования за лидером
Первоначально предполагалось, что каждый водитель согласует свою скорость со скоростью впереди идущего автомобиля:
где τ – время согласования скоростей (рис. 2.3), точки над координатой обозначают дифференцирование по времени.
Данная модель не описывает свойств неустойчивости, возникновения ударных волн и заторов. В левую часть уравнения (2.36) можно добавить задержку td, описывающую время реакции водителя на изменение скорости лидирующего автомобиля. Множитель 1/τ в этом уравнении интерпретируется как коэффициент чувствительности α, характеризующий скорость реакции водителя. Тогда (2.36) можно записать в виде дифференциально-разностного уравнения
При α=const условие неустойчивости уравнения (2.37) имеет вид td /τ > 1/2. Наличие неустойчивости позволяет моделировать ударные волны и заторы, но предположение о неизменности чувствительности не позволяет воспроизвести фундаментальную диаграмму. Более адекватная модель получается при учете возрастания чувствительности с уменьшением дистанции до лидирующего автомобиля. С этой точки зрения уравнение (2.37) может быть преобразовано к виду
Оценка коэффициентов n 1 и n 2 проводится по экспериментальным данным. В простейшем случае, используемом для теоретического анализа, n 1=0, n 2=1
После интегрирования уравнения (2.39) получаем
где kmax – константа, описывающая движение автомобилей в плотном потоке на очень близком расстоянии "бампер-к-бамперу". Когда транспортный поток является стационарным, плотность k выражается формулой k =1/(xi (t) – xi +1(t)), а так как скорость в стационарном режиме постоянна, то
Теория следования за лидером слишком детальна для ее использования при анализе движения в больших городских транспортных системах, но она является достаточным инструментом микроскопического моделирования транспортного потока, а также часто используется для анализа характеристик потока на различных пересечениях, перекрестках и т.д.
|

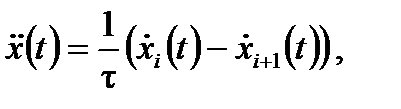 (2.36)
(2.36)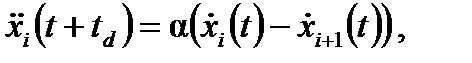 (2.37)
(2.37)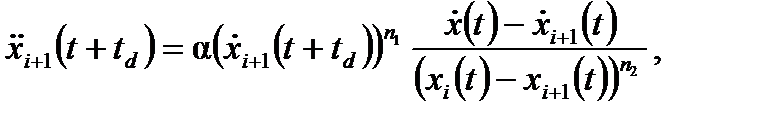 (2.38)
(2.38) (2.39)
(2.39) (2.40)
(2.40)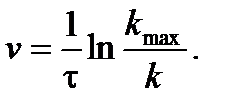 (2.41)
(2.41)


