Закон сохранения транспортного потока
При равновесном движении с плотностью автомобилей k (x, t) в направлении x число автомобилей в интервале длины дороги (x 1, x 2) в момент времени t равно
Пусть v (x, t) – скорость автомобилей в точке x в момент времени t. Число проходящих через x (единицу длины) автомобилей в момент t равно k (x, t) v (x, t). Найдем уравнение изменения плотности. Число автомобилей в интервале (x 1, x 2) за время t изменяется в соответствии с числом въезжающих и выезжающих машин:
Интегрируя по времени и полагая, что k и v – непрерывные функции, получим
Поскольку x 1, x 2 и t 1, t 2 > 0 произвольны,
Это уравнение дополняется начальным условием
Найдем уравнение для скорости v. Положим, что v зависит только от плотности k. Если дорога пуста (k =0), автомобили едут с максимальной скоростью v = v max. При наполнении дороги скорость падает вплоть до полной остановки (v =0), когда машины расположены "бампер-к-бамперу" (k = k max). Эта простейшая модель выражается следующим линейным соотношением
Тогда уравнение (2.16) принимает вид
и является законом сохранения количества автомобилей. Действительно, интегрируя (2.19) по x, получим
и, следовательно, количество автомобилей на отрезке дороги (x 1, x 2) постоянно для любых значений t ≥ 0. Уравнение (2.18), впервые полученное Гриншилдсом, носит его имя. Линейная аппроксимация Гриншилдса представлена на рис. 2.1.
Можно построить макроскопическую модель, в которой уравнение Гриншилдса является частным случаем. Рассмотрим связь между скоростью v и плотностью k автомобилей на дороге. В общем случае, когда плотность k повышается, водители снижают скорость и наоборот, поэтому
где x (t) – координата движения элемента потока. Проследим изменение скорости для некоторого передвигающегося элемента потока во времени, которое определяется как полная производная по времени
Из уравнения (2.16) следует соотношение
которое после подстановки в (2.23) принимает вид
Поскольку в соответствии с уравнениям (2.21)
из соотношения (2.24) получаем
где
где С – неотрицательная константа с размерностью скорости. Принято рассматривать более общий класс моделей, в которых
Уравнение (2.27) соответствует случаю n ≠–1, следовательно, из уравнений (2.26) и (2.27)
при n =–1 и
при n ≠–1. Формула (2.29) впервые получена Гринбергом и носит его имя. Обозначив v 0 – скорость при k =0, для значений n ≤0 можно записать
Следует отметить, что полученное ранее уравнение Гриншилдса (2.18) является частным случаем уравнения Гринберга (2.31) при n =1.
|
(2.13)
(2.14)
(2.15)
(2.16)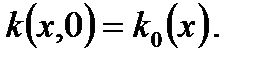
(2.17)
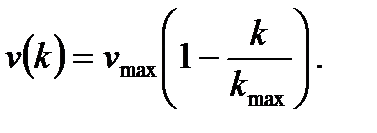(2.18)
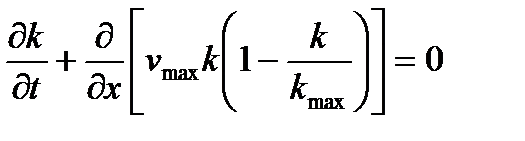(2.19)
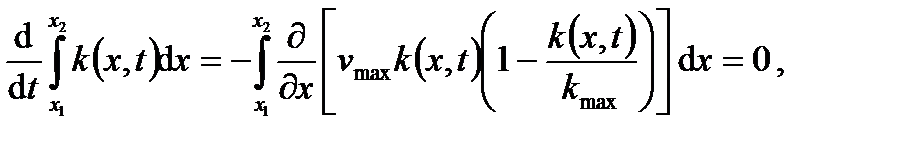(2.20)
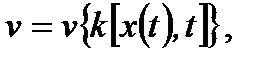(2.21)
(2.22)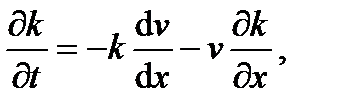
(2.23)
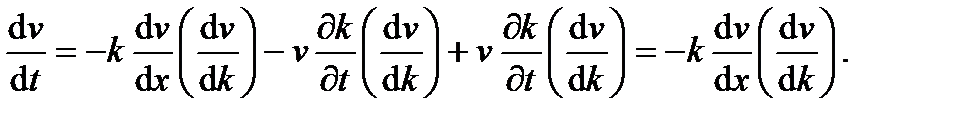(2.24)
(2.25)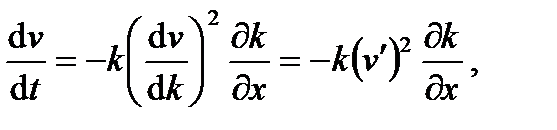
(2.26)
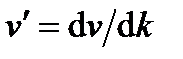, а отрицательный коэффициент пропорциональности 
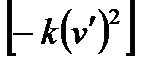можно интерпретировать как вязкость в жидкости. Для классической сжимаемой жидкости уравнение (2.26) называется уравнением Эйлера, в этом случае:
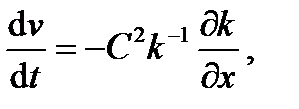(2.27)
(2.28)
. Решением этого уравнения будет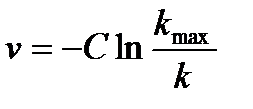
(2.29)
(2.30)
(2.31)
