Клеточные автоматы
Клеточный автомат – это математическая модель, представляющая идеализированную физическую систему, в которой пространство и время дискретны, а множества значений физических величин конечны. В простейшем виде клеточные автоматы представляют собой двумерную сетку произвольного размера, состоящую из ячеек. Состояние сетки (конфигурация) обновляется с течением времени, причём состояние каждой ячейки в следующий момент времени зависит от состояния ближайших её соседей (смежных ячеек) и, возможно, от её собственного состояния на текущей итерации. Количество возможных состояний ячейки конечно. Обновление конфигурации происходит параллельно, в соответствии с определёнными для данной модели правилами. При применении клеточного автомата для моделирования движения транспортного потока исследуемый участок дорожного пути формализуется в виде двумерной матрицы. Число строк матрицы равно числу полос движения моделируемого участка, а число столбцов определяется исходя из принятого масштаба клетки и общей протяжённости дороги, рис. 2.4. Как правило, масштаб выбирается таким образом, чтобы в клетку по длине вмещался точно один автомобиль с учётом безопасного расстояния до транспортных средств в соседних клетках. В любой момент времени каждая ячейка может быть либо пуста, либо занята транспортным средством.
Время в модели дискретно, значение размера шага обновления принимается из диапазона от 0,6 до 1,2 секунд, что приблизительно соответствует времени реакции водителя на изменение дорожной ситуации. Позиция автомобиля однозначно определяется номером строки – принятой полосой движения – и номером столбца – текущей координатой на отрезке транспортного пути. В ходе моделирования на каждом шаге эксперимента ко всем автомобилям параллельно и независимо применяются принятые в модели правила обновления состояний. Например, для воспроизведения трафика однополосной магистрали при переходе к новому состоянию все транспортные средства параллельно и независимо друг от друга обновляют значения скорости и координаты в соответствии с последовательным выполнением следующих шагов: 1. Ускорение. Если скорость i -го транспортного средства меньше предельного значения vi(t)< v max и расстояние до следующего впереди автомобиля Δ xi (t) больше vi(t)+1: Δ xi (t) > viΔt+1, то скорость следует увеличить на единицу:
2. Торможение. Если Δ xi (t) ≤ viΔt+1, тогда новое значение скорости:
3. Случайные воздействия. С заданной вероятностью скорость транспортного средства уменьшается на единицу:
при условии, что текущее значение положительно (vi(t)>0). 4. Передвижение. Транспортное средство перемещается вперёд на vi (t +1) ячеек:
Естественное желание водителей двигаться быстрее, не превышая максимально возможное на данном участке дороги значение скорости, формализует правило 1. Правило 2, торможение, обеспечивает отсутствие столкновений при превышении скорости. Правило 3 определяет стохастический характер модели: отсутствие вероятности делало бы моделирование полностью детерминированным – точно предсказуемым на любом шаге при известных начальных значениях переменных, – что недопустимо при воспроизведении динамики реального транспортного движения. Достоинство модели клеточных автоматов состоит в отсутствии сгустков и заторов, автомобили продолжают движение на минимальных скоростях и при большой плотности. Применение клеточных автоматов в моделировании дорожного движения является перспективным направлением, характеризуемым высокой вычислительной скоростью и эффективностью. Этот подход может быть классифицирован как имитационный и позволяет представлять динамику системы во времени. Кроме того, разделение машин по типам в этом случае является простой задачей, что отличает его от аналитических моделей. Однако у этих моделей есть некоторые недостатки: исключаются резкие изменения параметров движения при малых плотностях потока; из-за последовательного обновления заторы становятся неустойчивыми; скорость автомобилей не согласуется с реальными данными, особенно в режимах пробок.
Вопросы для самоконтроля 1. Назовите объекты микро- и макроскопического моделирования транспортных средств. 2. Что характеризуют основные параметры: интенсивность, состав и плотность транспортного потока? 3. Как подразделяют транспортные потоки по степени стесненности? 4. От чего зависит максимальная конструктивная скорость автомобиля? 5. Как связаны в пределах некоторого диапазона скорость, интенсивность и плотность транспортного потока? 6. Как связаны пространственная и временная плотности распределения скоростей? 7. Закон сохранения транспортного потока. 8. Аппроксимация зависимости скорости транспортного потока от его плотности по Гриншилдсу. 9. Зависимость скорости транспортного потока от его плотности по Гринбергу. 10. Фундаментальная диаграмма транспортного потока, модель Лайтхилла-Уизема. 11. Микроскопические модели: модель следования за лидером. 12. Микроскопические модели: модель клеточных автоматов.
|

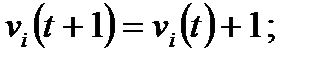 (2.42)
(2.42) (2.43)
(2.43) (2.44)
(2.44) (2.45)
(2.45)


