Кинематические волны в транспортном потоке
Зависимость интенсивности движения от плотности называют фундаментальной диаграммой транспортного потока. Эта диаграмма может быть получена по модели Лайтхилла-Уизема при следующих допущениях: · транспортный поток непрерывен, его плотность k (x, t) есть число машин, занимающих единицу длины дороги; · интенсивность движения q (x, t) равна числу машин, пересекающих черту x за единицу времени, определяется локальной плотностью k:
· скорость потока · на участке дороги без съездов-въездов количество машин сохраняется. Уравнения (2.32) и (2.19) образуют полную систему. После подстановки получим
где Соотношение q (k)= kvв (k) играет важную роль в теории транспортных потоков и называется фундаментальной диаграммой (рис. 2.2). В модели Лайтхилла-Уизема эта зависимость непрерывна, следовательно, предельная пропускная способность участка дороги определяется плотностью потока. Общий вид решения нелинейного уравнения (2.33):
где F – произвольная функция. Соотношение (2.34) описывает бегущую волну, рассматриваемую как волну уплотнения в среде. Волны типа (2.34) называют кинематическими волнами, что подчеркивает их кинематическое происхождение в противоположность динамической природе акустических и упругих волн.
|
(2.32)
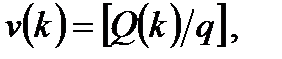т.е. средняя скорость является функцией плотности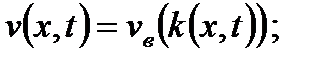 
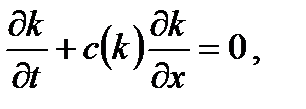(2.33)
– скорость распространения возмущений.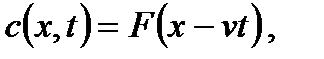
(2.34)
