Уравнение прямолинейного движения автомобиля
При движении автомобиля мощность двигателя затрачивается на выполнение работы по преодолению сопротивлений движению, рассмотренных в предыдущем параграфе. При передаче энергии от двигателя к ведущим колесам часть ее расходуется на преодоление сил трения в трансмиссии и на разгон масс двигателя. Поэтому суммарный момент на ведущих колесах автомобиля
Придадим центру масс автомобиля возможное перемещение
Подставим значения М к.в и из выражений (5.10) и (5.12) и выразим δφ через δ х. Тогда
Объединим все члены этого выражения, содержащие ускорение автомобиля
и обозначим полученную сумму Fj a:
Введем обозначения:
Величину m а.пр называют приведенной массой автомобиля. Кинетическая энергия поступательного движения этой массы равна сумме кинетических энергий всех масс автомобиля в их действительных движениях. Коэффициент δп.м – коэффициент приведенной массы – учитывает влияние относительного движения масс двигателя и колес на изменение кинетической энергии автомобиля, т.е. показывает, во сколько раз энергия, затрачиваемая на разгон масс реального автомобиля, больше энергии, необходимой для разгона поступательно движущегося твердого тела массой m а. Сила Fj a представляет собой приведенную силу инерции автомобиля, приложенную в его центре масс и эквивалентную силам инерции и инерционным моментам всех механизмов автомобиля при неустановившемся прямолинейном движении. Иными словами, сила Fj a в рассматриваемых условиях движения эквивалентна совокупности силы Fj п и моментов Мj к и Мj д. Учитывая выражения (5.16)...(5.18) и подставляя значения Mf и Fh, уравнение движения автомобиля можно записать в виде
Второе слагаемое правой части уравнения (5.19) характеризует суммарное сопротивление дороги (сопротивления подъему и качению). При малых значениях α, характерных для автомобильных дорог с твердым покрытием, можно принять cos α = 1, sin α = tg α = h и ввести обозначение
где ψ – коэффициент суммарного дорожного сопротивления. Подставим значение Fw в уравнение (5.19), пренебрегая скоростью ветра, и получим следующее уравнение движения автомобиля:
Это уравнение позволяет проанализировать влияние параметров автомобиля на характеристики движения и дать оценку показателей его тягово-скоростных свойств в конкретных дорожных условиях. При анализе движения автопоезда в уравнения (5.19) и (5.21) дополнительно включается сила сопротивления движению прицепа:
где m п – масса прицепа; δп.м.пр – коэффициент приведенной массы прицепа; Fw пр – сила сопротивления воздуха движению прицепа. Если рассматривать движение автопоезда как единой системы, целесообразно использовать уравнение, аналогичное уравнению (5.21):
где δп.м.ап – коэффициент приведенной массы автопоезда (отличается от δп.м учетом моментов инерции колес прицепа); m ап – масса автопоезда; kw ап – коэффициент сопротивления воздуха, kw ап=(1,2...1,3) kw. Если значения моментов инерции J д и J к неизвестны, то δп.м (или δп.м.ап) определяют по эмпирической формуле
где δ1 = 0,03...0,05; δ2 = 0,04...0,06; u к.п – передаточное число коробки передач; m а – полная масса автомобиля (автопоезда); m – фактическая масса автомобиля. Для случая движения автомобиля с отсоединенным от трансмиссии двигателем (накат, торможение) δ2 = 0, тогда δп.м ≈ 1,05.
|

 (5.12)
(5.12) . Колеса при этом получат возможные перемещения
. Колеса при этом получат возможные перемещения 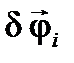 , (см. рис. 5.1). Предположим, что радиусы качения всех колес одинаковы и равны и отсутствует скольжение колес относительно дороги. Тогда
, (см. рис. 5.1). Предположим, что радиусы качения всех колес одинаковы и равны и отсутствует скольжение колес относительно дороги. Тогда 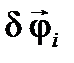 для всех колес будут одинаковыми, причем
для всех колес будут одинаковыми, причем 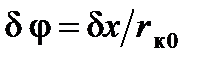 . Используя схему, приведенную на рис. 5.1, составим общее уравнение динамики. Работу всех сил и моментов на принятых возможных перемещениях определим, учитывая взаимные направления векторов сил и моментов и соответствующих им векторов перемещений:
. Используя схему, приведенную на рис. 5.1, составим общее уравнение динамики. Работу всех сил и моментов на принятых возможных перемещениях определим, учитывая взаимные направления векторов сил и моментов и соответствующих им векторов перемещений: (5.13)
(5.13)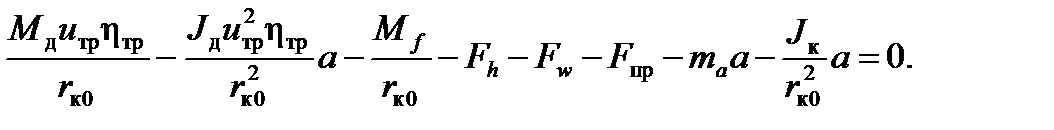 (5.14)
(5.14) (5.15)
(5.15) (5.16)
(5.16) (5.17)
(5.17) (5.18)
(5.18)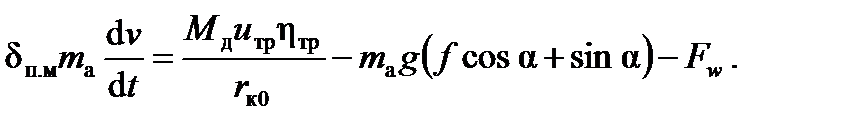 (5.19)
(5.19) (5.20)
(5.20) (5.21)
(5.21)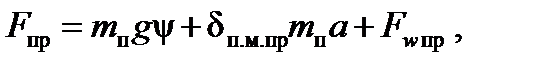 (5.22)
(5.22) (5.23)
(5.23)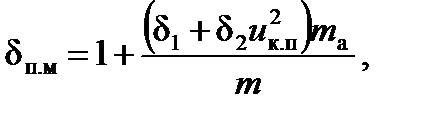 (5.24)
(5.24)


