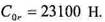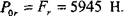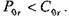РАСЧЕТ ПОДШИПНИКОВ КАЧЕНИЯ
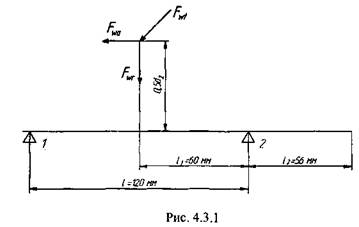
Подобрать подшипники качения для опор выходного вала червячного редуктора (рис. 4.3.1).
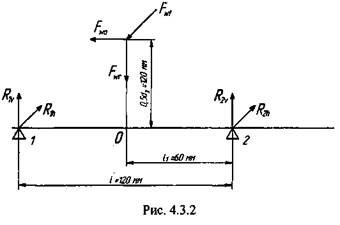
Частота вращения вала: диаметр в месте посадки подшипников: диаметр червячного колеса: температура подшипников: требуемый ресурс работы при вероятности безотказной работы 90%: режим нагружения: Силы в зацеплении: окружная радиальная осевая Радиальная сила на валу от муфты Расчет На начальном этапе необходимо определить силы, нагружающие каждый из подшипников. Реакции опор можно представить в виде проекций на две взаимно перпендикулярные плоскости, как это показано на рис. 4.3.2. Одну из этих плоскостей назовем вертикальной (все относящиеся к ней величины будем снабжать индексом «v»), a другую— горизонтальной (индекс «h»). Точки приложения и направление реактивных сил, возникающих от усилий в зацеплении, показаны на рис. 4.3.2. 208 Глава 4. Типовые элементы машин Точку приложения внешних сил можно перенести в точку О, лежащую на оси вращения вала. По правилам механики при таком переносе необходимо добавить момент вращения
Запишем условие равновесия моментов в горизонтальной и вертикальной плоскостях.
В горизонтальной плоскости окружная сила относительно опор приложена симметрично, следовательно, реакции в опорах равны между собой и составляют половину величины окружной силы, 4.3. Расчет подшипников качения 209
Реакции от силы
Реакции опор для расчета подшипников (принимается, что реакции опор от действия силы
зацеплении): Первоначально выбираем шариковый радиально-упорный однорядный подшипник 46109 особо легкой нормальной серии с углом контакта По справочным таблицам [7] определяем динамическую грузоподъемность выбранного подшипника:
Для радиально-упорного подшипника характерно наличие осевой нагрузки от приложения радиальных нагрузок, величины которых можно рассчитать как где е = 0,68 — зависящий от типа подшипника и угла контакта параметр осевой нагрузки (табл. 10.4.9). Учитывая схему установки подшипников и направление осевой силы, вычисляем осевые реакции в опорах:
Воспользовавшись формулой 10.4.51, для каждого из подшипников определим эквивалентную динамическую нагрузку
Здесь
X и Y — коэффициенты приведения радиальной и осевой сил. Рассчитаем коэффициенты радиальной и осевой сил для каждой из опор.
Опора 1: Как видно, более нагруженным является левый подшипник (опора /). Для него необходимо определить скорректированный по уровню надежности и условиям применения расчетный ресурс (10.4.44):
где
4.3. Расчет подшипников качения 211
Подставляя числовые значения, получаем:
Делаем вывод о том, что подшипник 46109 не пригоден к применению в данных условиях работы, так как его расчетный ресурс меньше требуемого: Проверим, не подойдет ли подшипник 46209 легкой серии того же типа и с тем же углом
т. е. условие ных целей пригоден. Теперь необходимо проверить-выбранный подшипник на статическую прочность. Условие статической прочности 10.4.32 для радиально-упорного подшипника записывается в виде
где (10.4.38); Пользуясь данными таблиц 10.4.1, 10.4.2 и [7], для подшипника 46209 получаем:
Тогда
ем Так как эквивалентная нагрузка не может быть меньше радиальной, то принима-
Следовательно, условие статической прочности выполнено: Таким образом, для данной задачи окончательно выбираем подшипник 46209. 212 Глава 4. Типовые элементы машин
|


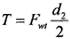 и момент изгиба.
и момент изгиба. 
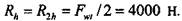



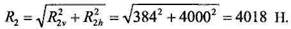


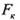 (рис. 4.3.3):
(рис. 4.3.3):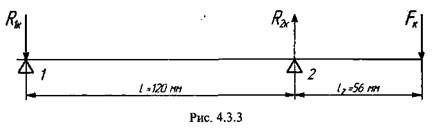
 совпадают по направлению с суммарными реакциями опор от сил в
совпадают по направлению с суммарными реакциями опор от сил в

 = 26°. Схема установки подшипников— «в распор», или схема X. Выбор подшипника с большим углом контакта обусловлен тем, что осевая сила в зацеплении червячного колеса составляет значительную часть от радиальной нагрузки.
= 26°. Схема установки подшипников— «в распор», или схема X. Выбор подшипника с большим углом контакта обусловлен тем, что осевая сила в зацеплении червячного колеса составляет значительную часть от радиальной нагрузки.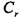 = 22500 Н.
= 22500 Н.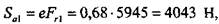

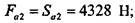
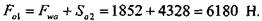

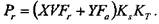
 — зависящий от характера нагрузки коэффициент безопасности (табл.
— зависящий от характера нагрузки коэффициент безопасности (табл.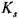 = 1;
= 1; — температурный коэффициент (табл. 10.4.8), который для рассматривае
— температурный коэффициент (табл. 10.4.8), который для рассматривае = 1, т. к. температура работы подшипников
= 1, т. к. температура работы подшипников — коэффициент вращения, имеющий значение
— коэффициент вращения, имеющий значение  = 1, поскольку относительно нагрузки вращается внутреннее кольцо подшипника;
= 1, поскольку относительно нагрузки вращается внутреннее кольцо подшипника;
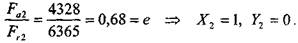


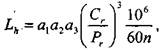
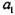 — коэффициент надежности, для вероятности безотказной работы 90% равный
— коэффициент надежности, для вероятности безотказной работы 90% равный  = 1;
= 1; — коэффициент, зависящий от специальных свойств подшипника, в данном
— коэффициент, зависящий от специальных свойств подшипника, в данном = 1;
= 1; — коэффициент, зависящий от условий работы подшипника, здесь принима
— коэффициент, зависящий от условий работы подшипника, здесь принима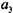 = 1.
= 1.
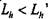 = 20000 часов.
= 20000 часов.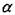 = 26°. Для этого подшипника параметр осевой нагрузки е и коэффициенты X и Y остаются неизменными, а динамическая грузоподъемность возрастает:
= 26°. Для этого подшипника параметр осевой нагрузки е и коэффициенты X и Y остаются неизменными, а динамическая грузоподъемность возрастает: 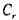 = 38700 Н. Тогда расчетный ресурс
= 38700 Н. Тогда расчетный ресурс
 выполняется. Следовательно, подшипник 46209 для заявлен-
выполняется. Следовательно, подшипник 46209 для заявлен-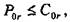
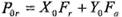 — эквивалентная статическая радиальная нагрузка
— эквивалентная статическая радиальная нагрузка —статическая грузоподъемность.
—статическая грузоподъемность.