В основне рівняння м.к.т. газів входить середня кінетична енергія поступального руху однієї молекули газу
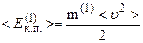 , (2.11)
, (2.11)
де середній квадрат швидкості молекули
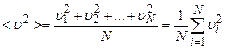 .
.
Введемо за означенням середню квадратичну швидкість молекули
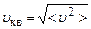 . (2.12)
. (2.12)
З урахуванням останнього вираз (2.11) запишемо так:
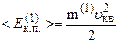 . (2.13)
. (2.13)
Порівняємо тепер співвідношення (2.10) і (2.7). Маємо

або
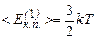 . (2.14)
. (2.14)
Звідси видно, що 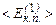 прямопропорційна абсолютній температурі газу і залежить лише від неї. Значить температура є мірою середньої кінетичної енергії поступального руху молекул ідеального газу; саме формула (2.14) дала можливість такого молекулярно-кінетичного трактування абсолютної температури. Оскільки температура – міра середньої величини енергії, то про температуру однієї чи кількох молекул не говорять. При
прямопропорційна абсолютній температурі газу і залежить лише від неї. Значить температура є мірою середньої кінетичної енергії поступального руху молекул ідеального газу; саме формула (2.14) дала можливість такого молекулярно-кінетичного трактування абсолютної температури. Оскільки температура – міра середньої величини енергії, то про температуру однієї чи кількох молекул не говорять. При 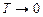
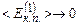 , тобто при абсолютному нулю температури припиняється поступальний рух молекул, а, отже, зникає тиск газу, що спричиняється ударами молекул об стінки посудини. Однак досягти абсолютного нуля неможливо.
, тобто при абсолютному нулю температури припиняється поступальний рух молекул, а, отже, зникає тиск газу, що спричиняється ударами молекул об стінки посудини. Однак досягти абсолютного нуля неможливо.
Оскільки величина 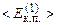 не залежить від маси молекули, то стає зрозумілим, чому в суміші газів окремі компоненти створюють незалежно парціальні тиски
не залежить від маси молекули, то стає зрозумілим, чому в суміші газів окремі компоненти створюють незалежно парціальні тиски 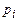 (див. закон Дальтона).
(див. закон Дальтона).
Знайдемо тепер формулу для розрахунку величини середньої квадратичної швидкості хаотичного теплового руху молекул газу. Для цього прирівняємо праві частини співвідношень (2.13) і (2.14):
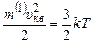 ,
,
звідки
 . (2.15)
. (2.15)
Оскільки  , а
, а 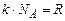 , то поділивши останнє рівняння на попереднє, маємо
, то поділивши останнє рівняння на попереднє, маємо 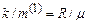 . Тоді
. Тоді
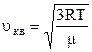 . (2.16)
. (2.16)
Якщо вираз (2.15) дозволяє розрахувати 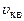 через масу молекули газу
через масу молекули газу 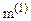 , то (2.16) – через молярну масу
, то (2.16) – через молярну масу  . Розрахунок на основі (2.16), наприклад, для азоту за нормальних умов дає
. Розрахунок на основі (2.16), наприклад, для азоту за нормальних умов дає 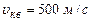 , для водню –
, для водню –  .
.
Виведемо ще одну форму запису основного рівняння м.к.т. газів. Домноживши рівняння (2.10) на об’єм V, маємо
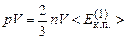 .
.
Але nV=N (див. означення (2.6)), а згідно з виразом (2.11) з урахуванням означення 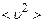
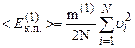 ,
,
тому
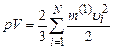 .
.
У свою чергу 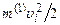 – це кінетична енергія поступального руху і-ї молекули газу, а
– це кінетична енергія поступального руху і-ї молекули газу, а 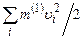 – кінетична енергія поступального руху всіх молекул газу
– кінетична енергія поступального руху всіх молекул газу 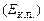 , тому остаточно
, тому остаточно
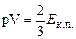 . (2.17)
. (2.17)

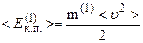 , (2.11)
, (2.11)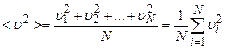 .
.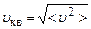 . (2.12)
. (2.12)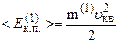 . (2.13)
. (2.13)
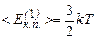 . (2.14)
. (2.14)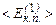 прямопропорційна абсолютній температурі газу і залежить лише від неї. Значить температура є мірою середньої кінетичної енергії поступального руху молекул ідеального газу; саме формула (2.14) дала можливість такого молекулярно-кінетичного трактування абсолютної температури. Оскільки температура – міра середньої величини енергії, то про температуру однієї чи кількох молекул не говорять. При
прямопропорційна абсолютній температурі газу і залежить лише від неї. Значить температура є мірою середньої кінетичної енергії поступального руху молекул ідеального газу; саме формула (2.14) дала можливість такого молекулярно-кінетичного трактування абсолютної температури. Оскільки температура – міра середньої величини енергії, то про температуру однієї чи кількох молекул не говорять. При 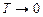
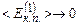 , тобто при абсолютному нулю температури припиняється поступальний рух молекул, а, отже, зникає тиск газу, що спричиняється ударами молекул об стінки посудини. Однак досягти абсолютного нуля неможливо.
, тобто при абсолютному нулю температури припиняється поступальний рух молекул, а, отже, зникає тиск газу, що спричиняється ударами молекул об стінки посудини. Однак досягти абсолютного нуля неможливо.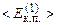 не залежить від маси молекули, то стає зрозумілим, чому в суміші газів окремі компоненти створюють незалежно парціальні тиски
не залежить від маси молекули, то стає зрозумілим, чому в суміші газів окремі компоненти створюють незалежно парціальні тиски 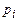 (див. закон Дальтона).
(див. закон Дальтона).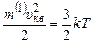 ,
, . (2.15)
. (2.15) , а
, а 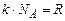 , то поділивши останнє рівняння на попереднє, маємо
, то поділивши останнє рівняння на попереднє, маємо 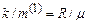 . Тоді
. Тоді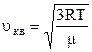 . (2.16)
. (2.16)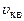 через масу молекули газу
через масу молекули газу 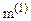 , то (2.16) – через молярну масу
, то (2.16) – через молярну масу  . Розрахунок на основі (2.16), наприклад, для азоту за нормальних умов дає
. Розрахунок на основі (2.16), наприклад, для азоту за нормальних умов дає 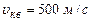 , для водню –
, для водню –  .
.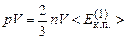 .
.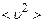
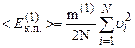 ,
,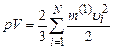 .
.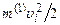 – це кінетична енергія поступального руху і-ї молекули газу, а
– це кінетична енергія поступального руху і-ї молекули газу, а 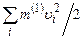 – кінетична енергія поступального руху всіх молекул газу
– кінетична енергія поступального руху всіх молекул газу 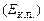 , тому остаточно
, тому остаточно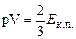 . (2.17)
. (2.17)


