Рух ідеальної рідини. Рівняння нерозривності. Рівняння Бернуллі
Щоб описати рух частинок рідини або газу можна для кожної точки простору задати вектор швидкості як функцію часу. Сукупність векторів
Розглянемо трубку течії, настільки тонку, що в кожному її перерізі швидкість можна вважати однаковою у всіх точках перерізу (Рис.1.22). Можна показати, що
або
Рівняння (1.101) називають рівнянням нерозривності, з якого слідує, що чим більша площа перерізу трубки течії, тим менша швидкість течії і навпаки. Коли рідина рухається по трубі змінного перерізу і різної висоти (рис. 1.23), то для деякого її об’єму змінюється як кінетична так і потенціальна енергії об’єму рідини. Ця зміна обумовлена дією деяких зовнішніх сил, робота яких рівна зміні потенціальної і кінетичної енергії рідини
Після підстановок і перетворень в лівій та правій частинах останнього співвідношення отримаємо вираз
або для довільного перерізу
де Рівняння (1.103) вивів Бернуллі і воно носить його ім’я. Це рівняння виражає закон збереження енергії при стаціонарній течії ідеальної рідини. Для горизонтальної трубки течії
Струмінь води, що витікає з бічного отвору посудини створює реактивну тягу, і якщо посудину поставити на візок, то останній почне рухатись разом з посудиною під дією цієї сили
|

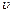 , заданих для всіх точок простору, утворює поле вектора швидкості. Якщо провести лінії, дотичні до яких співпадають з напрямком вектора швидкості в кожній точці, то ми отримаємо лінії течії. Поверхню, утворену лініями течії, що проведені через усі точки малого замкнутого контура, називають трубкою течії.
, заданих для всіх точок простору, утворює поле вектора швидкості. Якщо провести лінії, дотичні до яких співпадають з напрямком вектора швидкості в кожній точці, то ми отримаємо лінії течії. Поверхню, утворену лініями течії, що проведені через усі точки малого замкнутого контура, називають трубкою течії. Розрізняють ламінарну або шарувату течію та турбулентну. Ламінарною називають течію, в якій окремі шари при своєму русі не перемішуються (Рис.1.21а). в турбулентній течії відбувається перемішування окремих шарів, утворення завихрень в результаті виникнення нормальної (поперечної) складової швидкості (Рис.1.21б).
Розрізняють ламінарну або шарувату течію та турбулентну. Ламінарною називають течію, в якій окремі шари при своєму русі не перемішуються (Рис.1.21а). в турбулентній течії відбувається перемішування окремих шарів, утворення завихрень в результаті виникнення нормальної (поперечної) складової швидкості (Рис.1.21б). В реальних рідинах між окремими шарами рідини виникають сили в’язкого (внутрішнього) тертя. В окремих випадках вплив внутрішнього тертя невеликий і ним можна знехтувати. Абсолютно нестисливу і нев’язку рідину називають – ідеальною.
В реальних рідинах між окремими шарами рідини виникають сили в’язкого (внутрішнього) тертя. В окремих випадках вплив внутрішнього тертя невеликий і ним можна знехтувати. Абсолютно нестисливу і нев’язку рідину називають – ідеальною.
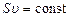 . (1.101)
. (1.101)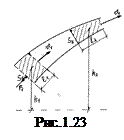
 .
.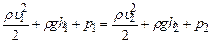 (1.102)
(1.102)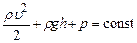 , (1.103)
, (1.103) – динамічний тиск,
– динамічний тиск, 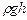 – гідростатичний тиск, р – статичний тиск.
– гідростатичний тиск, р – статичний тиск. і рівняння Бернуллі приймає вигляд
і рівняння Бернуллі приймає вигляд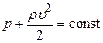 . (1.104)
. (1.104) Звідси випливає, що в тих місцях труби, де більша швидкість течії, тиск буде меншим і навпаки (Рис.1.24). Якщо рідину налити в посудину площею перерізу
Звідси випливає, що в тих місцях труби, де більша швидкість течії, тиск буде меншим і навпаки (Рис.1.24). Якщо рідину налити в посудину площею перерізу  , в бічній поверхні якої є отвір площею
, в бічній поверхні якої є отвір площею 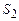 , то швидкість витікання рідини через отвір
, то швидкість витікання рідини через отвір  (1.105)
(1.105)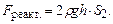 (1.106)
(1.106)


