Рівняння стану ідеального газу
Рівняння стану ідеального газу має три еквівалентні форми запису (при цьому маса газу m =const!). Перша з них – узагальнення експериментально встановлених законів Бойля-Маріота, Гей-Люсака і Шарля, відоме як рівняння Клапейрона:
(стала різна для різних газів і для різної кількості одного газу). Окремі випадки: а) Т =сonst, рівняння ізотерми pV =const; б) p =const, рівняння ізобари V/T =const; в) V =const, рівняння ізохори p/T =const. Закон Авогадро: при однакових тисках і однакових температурах в рівних об’ємах різних газів міститься однакове число молекул. Інше формулювання цього закону: при однакових тисках і однакових температурах молі різних газів займають однакові об’єми. Зокрема, при нормальних умовах ( Виходячи з закону Авогадро маємо, що в рівнянні (2.1) для
Вираз (2.2) – рівняння стану для одного моля ідеального газу. R – універсальна газова стала. Числове значення для R знайдемо з рівняння (2.2) при нормальних умовах:
Домножимо праву і ліву частину рівняння (2.2) на кількість речовини (
Співвідношення (2.3) – рівняння Менделєєва-Клапейрона. Це – друга форма запису рівняння стану ідеального газу. Визначаючи з рівняння
Введемо тепер сталу Больцмана
Підставляючи у праву частину (2.5) значення R та Виразимо тепер на основі рівності (2.5) універсальну газову сталу через k та NA і врахуємо, що
За означенням число молекул в одиниці об’єму – це концентрація молекул:
Вираз (2.7) – третя форма запису рівняння стану ідеального газу (через концентрацію). Відмітимо ще два факти, пов’язані з концентрацією: а) концентрація молекул ідеального газу за нормальних умов У випадку суміші
тобто тиск суміші газів рівний сумі парціальних тисків (закон Дальтона). Щоб розрахувати молярну масу суміші газів, розпишемо ліву і праву частину співвідношення (2.8), виходячи з рівняння Менделєєва-Клапейрона:
|

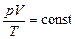 (2.1)
(2.1)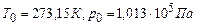 ) молярний об’єм ідеального газу
) молярний об’єм ідеального газу 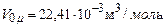
 величина сталої однакова для всіх газів. Позначивши її через R, одержимо
величина сталої однакова для всіх газів. Позначивши її через R, одержимо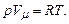 (2.2)
(2.2)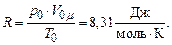
 ). Врахувавши, що
). Врахувавши, що  разів більший від об’єму одного моля
разів більший від об’єму одного моля 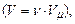 одержимо
одержимо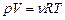 . (2.3)
. (2.3)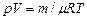 масу “ m ” газу і розділюючи одержаний вираз на об’єм, одержимо формулу для розрахунку густини газу
масу “ m ” газу і розділюючи одержаний вираз на об’єм, одержимо формулу для розрахунку густини газу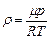 . (2.4)
. (2.4)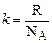 . (2.5)
. (2.5)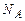 , одержимо
, одержимо 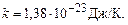
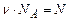 (число молекул). Маємо з рівняння (2.3):
(число молекул). Маємо з рівняння (2.3):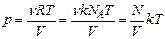 .
.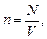 (2.6)
(2.6)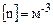 . З урахуванням цього попередня рівність набуде вигляду
. З урахуванням цього попередня рівність набуде вигляду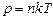 (2.7)
(2.7)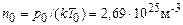 називається сталою Лошмідта; б) густину газу можна розраховувати як добуток концентрації і маси однієї молекули
називається сталою Лошмідта; б) густину газу можна розраховувати як добуток концентрації і маси однієї молекули 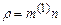 (це випливає з фізичного змісту величин
(це випливає з фізичного змісту величин 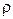 та n).
та n). газів число всіх молекул
газів число всіх молекул 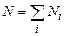 ,
, 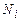 – число молекул і -го сорту. Тоді рівняння (2.7) з урахуванням (2.6) дає
– число молекул і -го сорту. Тоді рівняння (2.7) з урахуванням (2.6) дає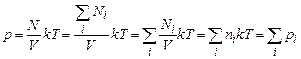 ,
,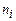 – концентрація молекул і -го сорту.
– концентрація молекул і -го сорту. 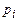 – парціальний тиск і -ї компоненти суміші, тобто тиск, який створював би даний (і -й) газ, якщо б він сам займав об’єм, рівний об’єму суміші при цій же температурі. Остаточно маємо
– парціальний тиск і -ї компоненти суміші, тобто тиск, який створював би даний (і -й) газ, якщо б він сам займав об’єм, рівний об’єму суміші при цій же температурі. Остаточно маємо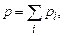 (2.8)
(2.8)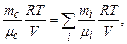
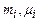 – відповідно, маса та молярна маса і-ї компоненти суміші;
– відповідно, маса та молярна маса і-ї компоненти суміші; 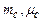 – маса та молярна маса суміші газів. З останнього рівняння маємо
– маса та молярна маса суміші газів. З останнього рівняння маємо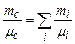 або
або 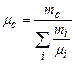 . (2.9)
. (2.9)


