Барометрична формула. Розподіл Больцмана частинок у потенціальному полі
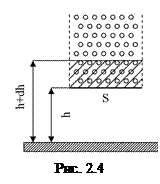
Атмосферний тиск на висоті h над Землею зумовлений вагою шарів повітря, що знаходяться на більших від h висотах. Позначимо тиск на висоті h через р. Тоді
F – вага циліндричного стовпа повітря, S – площа основи циліндра (див. рис.2.4). На висоті h + dh тиск буде p + dp, причому на основі виразу (2.19)
Із збільшенням висоти h вага верхнього стовпа повітря зменшується Далі
де dm – маса молекул повітря в заштрихованому елементарному об’ємі dV, g – прискорення вільнопадаючих тіл,
зміною Повітря мало відрізняється від ідеального газу при звичайних умовах, тому
(див. формулу (2.4) з відповідними позначеннями). Молярна маса повітря Підставимо вираз (2.21) у рівняння (2.20) і одержане співвідношення розділимо на р. В результаті маємо
Будемо вважати нижче величини Т і g незалежними від h (таке допущення годиться для невеликих висот). Тоді останнє рівняння є диференціальним рівнянням з розділеними змінними. Інтегруючи його, маємо
с – деяка постійна величина. Потенціюємо тепер одержане співвідношення і одержимо
Нехай на поверхні Землі (h=0) p=p0. Тоді с=р0 і остаточно маємо
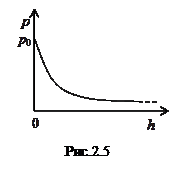
Формула (2.22) називається барометричною. З неї випливає, що тиск газу зменшується з висотою за експоненціальним законом, причому тим швидше, чим важчий газ і чим нижча температура. Залежність атмосферного тиску від висоти графічно відображена на рис.2.5. Оцінка на основі виразу (2.22) дає, що при підйомі на 6км тиск падає приблизно у два рази. Виразимо тепер у формулі (2.22) тиск через концентрацію молекул на основі рівняння стану (2.7):
(
Останній вираз дає розподіл концентрації молекул в залежності від висоти над Землею, а саме: із збільшенням висоти концентрація зменшується. Якби абсолютна температура була рівна нулю, то концентрація молекул в атмосфері теж була б рівною нулю, всі вони упали б на Землю під дією сили тяжіння. Саме хаотичний тепловий рух молекул утримує атмосферу. На висоті h кожна молекула володіє у полі тяжіння потенціальною енергією
Молекули розміщуються густіше там, де менша їх потенціальна енергія. Больцман довів, що розподіл частинок за їх потенціальними енергіями (2.24) є універсальним, тобто годиться для будь-якого потенціального поля сил, а не лише для поля тяжіння. Тому вираз (2.24) називають розподілом Больцмана.
|

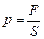 , (2.19)
, (2.19)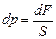 .
.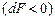 , а вага нижнього стовпчика (заштрихованого на рис. 2.4) зростає на стільки ж
, а вага нижнього стовпчика (заштрихованого на рис. 2.4) зростає на стільки ж  . Тому
. Тому 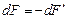 .
. ,
,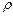 – густина повітря на висоті h. Видно, що при виведенні співвідношення
– густина повітря на висоті h. Видно, що при виведенні співвідношення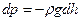 (2.20)
(2.20)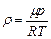 (2.21)
(2.21)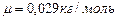 (визначена на основі співвідношення (2.9) з урахуванням процентного вмісту азоту, кисню та інших газів).
(визначена на основі співвідношення (2.9) з урахуванням процентного вмісту азоту, кисню та інших газів).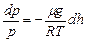 .
.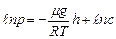 ,
,
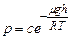 .
.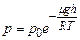 . (2.22)
. (2.22)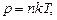
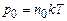
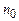 тут концентрація молекул на висоті
тут концентрація молекул на висоті 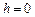 , а не стала Лошмідта!). Перейдемо також від молярної маси до маси однієї молекули за відомим зв’язком
, а не стала Лошмідта!). Перейдемо також від молярної маси до маси однієї молекули за відомим зв’язком 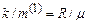 . Тоді матимемо
. Тоді матимемо . (2.23)
. (2.23)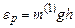 , тому співвідношення (2.23) можна записати ще так:
, тому співвідношення (2.23) можна записати ще так: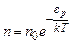 . (2.24)
. (2.24)


