В термодинаміці розглядають тільки такі системи, для яких механічна енергія системи як цілого не змінюється. За рахунок виконаної над системою роботи  та переданої їй кількості теплоти
та переданої їй кількості теплоти  змінюється лише внутрішня енергія термодинамічної системи
змінюється лише внутрішня енергія термодинамічної системи  :
:
 . (2.28)
. (2.28)
Тут 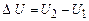 – приріст внутрішньої енергії (
– приріст внутрішньої енергії (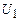 та
та  – початкове та кінцеве значення внутрішньої енергії). Співвідношення (2.28) відображає закон збереження і перетворення енергії стосовно теплових процесів.
– початкове та кінцеве значення внутрішньої енергії). Співвідношення (2.28) відображає закон збереження і перетворення енергії стосовно теплових процесів.
На відміну від механіки, де частіше приходилося обчислювати роботу зовнішніх сил, в термодинаміці, в основному, мають справу з роботою системи проти зовнішніх сил (А). Саме у зв’язку з цим ці величини тут перепозначені. Перейдемо тепер у рівнянні (2.28) від 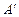 до
до  (
( на основі третього закону Ньютона) і розв’яжемо одержане рівняння відносно Q:
на основі третього закону Ньютона) і розв’яжемо одержане рівняння відносно Q:
 (2.29)
(2.29)
або в диференціальній формі
 . (2.30)
. (2.30)
 – елементарна кількість теплоти, так само як
– елементарна кількість теплоти, так само як  – елементарна робота;
– елементарна робота; 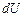 – елементарний приріст внутрішньої енергії.
– елементарний приріст внутрішньої енергії.
Співвідношення (2.29) (чи (2.30)) є математичним виразом першого начала (закону, принципу) термодинаміки. Формулювання цього принципу: кількість теплоти, наданої системі ззовні, витрачається на роботу системи проти зовнішніх сил і на збільшення внутрішньої енергії системи.
Не треба думати, що завжди за рахунок одержаного тепла внутрішня енергія системи збільшується. Може бути, що 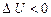 ; при цьому на основі (2.29)
; при цьому на основі (2.29) 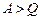 , тобто система виконує роботу як за рахунок одержаного тепла, так і за рахунок запасу внутрішньої енергії. Як і робота А, так і кількість теплоти Q є величина алгебраїчна: Q<;0 означає, що система віддає тепло зовнішньому середовищу (холодильнику), а Q>;0 означає, що система одержує тепло від нагрівника. Як і у випадку роботи, для кількості теплоти не можна писати
, тобто система виконує роботу як за рахунок одержаного тепла, так і за рахунок запасу внутрішньої енергії. Як і робота А, так і кількість теплоти Q є величина алгебраїчна: Q<;0 означає, що система віддає тепло зовнішньому середовищу (холодильнику), а Q>;0 означає, що система одержує тепло від нагрівника. Як і у випадку роботи, для кількості теплоти не можна писати  , бо останнє означало б, що значок варіації
, бо останнє означало б, що значок варіації 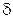 еквівалентний значку диференціала d, тобто що Q є функцією стану системи. Правильним є запис
еквівалентний значку диференціала d, тобто що Q є функцією стану системи. Правильним є запис  (сума елементарних кількостей теплоти рівна повній кількості теплоти). Тепер є очевидним, що інтегральна форма запису 1-го принципу термодинаміки (2.29) одержується з диференціальної (2.30), якщо останню проінтегрувати для деякого процесу, початок якого формально позначити “1”, а кінець – “2”:
(сума елементарних кількостей теплоти рівна повній кількості теплоти). Тепер є очевидним, що інтегральна форма запису 1-го принципу термодинаміки (2.29) одержується з диференціальної (2.30), якщо останню проінтегрувати для деякого процесу, початок якого формально позначити “1”, а кінець – “2”:
 .
.
Якісне формулювання 1-го принципу термодинаміки: неможливо побудувати періодично діючий двигун, який виконував би роботу більшу, ніж кількість переданої йому ззовні енергії (вічний двигун І-го роду неможливий).
Тепловий двигун, про який іде мова в якісному формулюванні принципу, це пристрій, що перетворює внутрішню енергію в механічну (“теплоту в роботу”). Основні частини такої установки – робоче тіло (газ, пара), нагрівник і холодильник. Періодично діючий двигун такий, що внаслідок процесу робоче тіло повертається за період до вихідного (початкового) стану; тоді 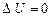 і
і 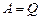 на основі (2.29).
на основі (2.29).
Застосуємо тепер 1-й принцип термодинаміки до ізопроцесів в ідеальному газі. Оскільки для ізохорного процесу  , то з рівняння (2.29) маємо, що
, то з рівняння (2.29) маємо, що 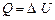 . Значить, при ізохорному процесі кількість теплоти, одержана газом ззовні, йде на збільшення внутрішньої енергії газу. При цьому температура газу підвищується (в наступному параграфі буде показано, що внутрішня енергія ідеального газу прямопропорційна абсолютній температурі).
. Значить, при ізохорному процесі кількість теплоти, одержана газом ззовні, йде на збільшення внутрішньої енергії газу. При цьому температура газу підвищується (в наступному параграфі буде показано, що внутрішня енергія ідеального газу прямопропорційна абсолютній температурі).
У випадку ізобаричного розширення ідеального газу  (див. попередній параграф); оскільки
(див. попередній параграф); оскільки 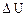 теж додатнє, бо
теж додатнє, бо 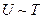 , то на основі (2.29)
, то на основі (2.29) 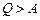 . Температура газу зростає. 1-й принцип термодинаміки для ізобаричного процесу формулюється як у загальному випадку.
. Температура газу зростає. 1-й принцип термодинаміки для ізобаричного процесу формулюється як у загальному випадку.
Для ізотермічного процесу робота газу розраховується за формулою (2.27). Оскільки 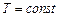 , то
, то 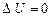 і вираз 1-го принципу (2.29) зводиться до наступного:
і вираз 1-го принципу (2.29) зводиться до наступного: 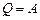 . Це означає, що при ізотермічному процесі кількість теплоти, одержана газом ззовні, йде на роботу газу проти зовнішніх сил.
. Це означає, що при ізотермічному процесі кількість теплоти, одержана газом ззовні, йде на роботу газу проти зовнішніх сил.

 та переданої їй кількості теплоти
та переданої їй кількості теплоти  змінюється лише внутрішня енергія термодинамічної системи
змінюється лише внутрішня енергія термодинамічної системи  :
: . (2.28)
. (2.28)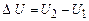 – приріст внутрішньої енергії (
– приріст внутрішньої енергії (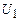 та
та  – початкове та кінцеве значення внутрішньої енергії). Співвідношення (2.28) відображає закон збереження і перетворення енергії стосовно теплових процесів.
– початкове та кінцеве значення внутрішньої енергії). Співвідношення (2.28) відображає закон збереження і перетворення енергії стосовно теплових процесів.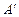 до
до  (
( на основі третього закону Ньютона) і розв’яжемо одержане рівняння відносно Q:
на основі третього закону Ньютона) і розв’яжемо одержане рівняння відносно Q: (2.29)
(2.29) . (2.30)
. (2.30) – елементарна кількість теплоти, так само як
– елементарна кількість теплоти, так само як  – елементарна робота;
– елементарна робота; 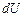 – елементарний приріст внутрішньої енергії.
– елементарний приріст внутрішньої енергії.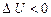 ; при цьому на основі (2.29)
; при цьому на основі (2.29) 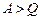 , тобто система виконує роботу як за рахунок одержаного тепла, так і за рахунок запасу внутрішньої енергії. Як і робота А, так і кількість теплоти Q є величина алгебраїчна: Q<;0 означає, що система віддає тепло зовнішньому середовищу (холодильнику), а Q>;0 означає, що система одержує тепло від нагрівника. Як і у випадку роботи, для кількості теплоти не можна писати
, тобто система виконує роботу як за рахунок одержаного тепла, так і за рахунок запасу внутрішньої енергії. Як і робота А, так і кількість теплоти Q є величина алгебраїчна: Q<;0 означає, що система віддає тепло зовнішньому середовищу (холодильнику), а Q>;0 означає, що система одержує тепло від нагрівника. Як і у випадку роботи, для кількості теплоти не можна писати  , бо останнє означало б, що значок варіації
, бо останнє означало б, що значок варіації 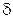 еквівалентний значку диференціала d, тобто що Q є функцією стану системи. Правильним є запис
еквівалентний значку диференціала d, тобто що Q є функцією стану системи. Правильним є запис  (сума елементарних кількостей теплоти рівна повній кількості теплоти). Тепер є очевидним, що інтегральна форма запису 1-го принципу термодинаміки (2.29) одержується з диференціальної (2.30), якщо останню проінтегрувати для деякого процесу, початок якого формально позначити “1”, а кінець – “2”:
(сума елементарних кількостей теплоти рівна повній кількості теплоти). Тепер є очевидним, що інтегральна форма запису 1-го принципу термодинаміки (2.29) одержується з диференціальної (2.30), якщо останню проінтегрувати для деякого процесу, початок якого формально позначити “1”, а кінець – “2”: .
.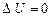 і
і 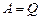 на основі (2.29).
на основі (2.29). , то з рівняння (2.29) маємо, що
, то з рівняння (2.29) маємо, що 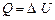 . Значить, при ізохорному процесі кількість теплоти, одержана газом ззовні, йде на збільшення внутрішньої енергії газу. При цьому температура газу підвищується (в наступному параграфі буде показано, що внутрішня енергія ідеального газу прямопропорційна абсолютній температурі).
. Значить, при ізохорному процесі кількість теплоти, одержана газом ззовні, йде на збільшення внутрішньої енергії газу. При цьому температура газу підвищується (в наступному параграфі буде показано, що внутрішня енергія ідеального газу прямопропорційна абсолютній температурі). (див. попередній параграф); оскільки
(див. попередній параграф); оскільки 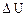 теж додатнє, бо
теж додатнє, бо 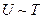 , то на основі (2.29)
, то на основі (2.29) 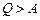 . Температура газу зростає. 1-й принцип термодинаміки для ізобаричного процесу формулюється як у загальному випадку.
. Температура газу зростає. 1-й принцип термодинаміки для ізобаричного процесу формулюється як у загальному випадку.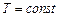 , то
, то 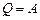 . Це означає, що при ізотермічному процесі кількість теплоти, одержана газом ззовні, йде на роботу газу проти зовнішніх сил.
. Це означає, що при ізотермічному процесі кількість теплоти, одержана газом ззовні, йде на роботу газу проти зовнішніх сил.


