Адіабатичний процес. Рівняння Пуасона
Адіабатичним (або адіабатним) називається процес, що протікає без теплообміну з навколишнім середовищем. Умова такого процесу:
тобто при адіабатичному розширенні газ виконує роботу за рахунок запасу його внутрішньої енергії. При цьому ідеальний газ охолоджується. Дійсно, взявши до уваги вираз для внутрішньої енергії (2.37), маємо
Звідси бачимо, що при розширенні газу (A>0) приріст температури Вираз (2.40) дозволяє розрахувати роботу ідеального газу при адіабатичному процесі. Якщо використати рівняння Менделєєва-Клапейрона, то цю роботу можна виразити через параметри p та V. Щоб здійснити адіабатичний процес, треба надійно теплоізолювати систему або здійснювати його дуже швидко, щоб теплообмін практично не встигав відбутися. Другий з цих варіантів зустрічається у природі. Наприклад, величезні маси атмосферного повітря, нагріваючись біля поверхні Землі, піднімаються вгору, потрапляють в області нижчих тисків і розширюються. Цей процес адіабатичний, бо через погану теплопровідність повітря теплообміном при цьому можна знехтувати. Виконуючи роботу розширення проти зовнішнього тиску, повітря охолоджується, а водяна пара перетворюється в насичену й конденсується (хмари). Згущення і розрідження, що утворюються у звуковій хвилі в газах, – це також по суті процеси адіабатичного стиснення і розширення газу. Оскільки швидкість поширення звуку немала (340м/с при кімнатних температурах), процеси тут відбуваються так швидко, що за цей короткий час теплообміном можна знехтувати. Приступимо тепер до виведення рівняння адіабати. За основу беремо вираз 1-го принципу термодинаміки для цього процесу (в диференціальній формі (2.30)):
Розпишемо ліву частину цього рівняння. Елементарну роботу
Елементарний приріст внутрішньої енергії dU запишемо, продиференціювавши вираз (2.37):
Тепер замість (2.41) маємо
Поділимо далі останнє рівняння на добуток
Коефіцієнт
де введено позначення
Тепер співвідношення (2.42) приймає вигляд
Оскільки
або Звідси випливає, що
Або
Співвідношення (2.44) є рівнянням адіабати або рівнянням Пуасона. Параметр
Згадаємо, що рівняння ізотерми Якщо з рівняння Менделєєва-Клапейрона або з рівняння (2.45) визначити об’єм V і підставити одержаний вираз у (2.44), то матимемо третю форму запису рівняння Пуасона
Зауваження: 1) рівняння Пуасона (2.44–46) правильні за умови, що кількість газу
|

 (або Q= 0). Застосовуючи до адіабатичного процесу 1-й принцип термодинаміки (2.29), маємо
(або Q= 0). Застосовуючи до адіабатичного процесу 1-й принцип термодинаміки (2.29), маємо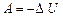 , (2.39)
, (2.39)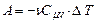 . (2.40)
. (2.40)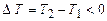 , в чому і треба було переконатися. Описане явище – спосіб отримання низьких температур.
, в чому і треба було переконатися. Описане явище – спосіб отримання низьких температур. . (2.41)
. (2.41)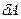 розрахуємо на основі формули (2.25), причому тиск підставимо, взявши його з рівняння Менделєєва-Клапейрона (2.3):
розрахуємо на основі формули (2.25), причому тиск підставимо, взявши його з рівняння Менделєєва-Клапейрона (2.3):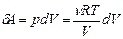 .
. .
.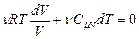 .
.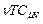 і одержимо
і одержимо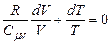 . (2.42)
. (2.42)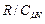 запишемо, виразивши газову сталу через різницю
запишемо, виразивши газову сталу через різницю  з рівняння Майєра (2.38):
з рівняння Майєра (2.38):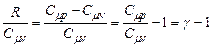 ,
,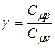 . (2.43)
. (2.43)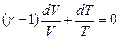 .
. , то наше рівняння запишеться у формі
, то наше рівняння запишеться у формі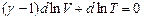
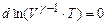 .
.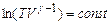
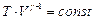 . (2.44)
. (2.44)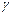 , введений вище, називається показником адіабати або коефіцієнтом Пуасона. Для повітря, наприклад,
, введений вище, називається показником адіабати або коефіцієнтом Пуасона. Для повітря, наприклад, 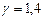 (в сухому повітрі 99% двохатомних молекул!). В загальному випадку
(в сухому повітрі 99% двохатомних молекул!). В загальному випадку  , оскільки
, оскільки 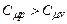 .
. Визначаючи абсолютну температуру з рівняння Менделєєва-Клапейрона і підставляючи одержаний вираз у співвідношення (2.44), одержимо іншу форму запису рівняння Пуасона:
Визначаючи абсолютну температуру з рівняння Менделєєва-Клапейрона і підставляючи одержаний вираз у співвідношення (2.44), одержимо іншу форму запису рівняння Пуасона: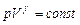 . (2.45)
. (2.45)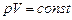 . Порівняння двох останніх виразів приводить до висновку, що адіабата графічно “крутіша” від ізотерми (див. рис.2.9).
. Порівняння двох останніх виразів приводить до висновку, що адіабата графічно “крутіша” від ізотерми (див. рис.2.9).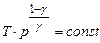 . (2.46)
. (2.46)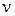 (чи його маса) незмінні під час процесу; 2) величини “const” у всіх виписаних рівняннях різні.
(чи його маса) незмінні під час процесу; 2) величини “const” у всіх виписаних рівняннях різні.


