Ентропія. Закон зростання ентропії
(див. (2.51) з відповідним роз’ясненням). Але, якщо криволінійний інтеграл по замкнутому контуру рівний нулю, то існує така функція від змінних інтегрування, що повний диференціал від неї дорівнює підінтегральному виразу. Значить, для оборотного термодинамічного процесу
Введену таким способом функцію S називають ентропією. Вона визначається лише станом системи і не залежить від шляху, яким система прийшла в цей стан (
(співвідношення (2.55) одержується шляхом інтегрування рівності (2.54)). Формули (2.54–55) дають прирости ентропії для оборотних процесів. Щоб знайти абсолютне значення S, треба скористуватися теоремою Нернста (третім принципом термодинаміки): ентропія тіла при Т =0 рівна нулю. Ентропія системи рівна сумі ентропій усіх тіл, що входять у систему. Оцінимо тепер зміну ентропії у випадку необоротного циклу. Нехай деякий цикл складається з двох процесів: необоротного АМВ та оборотного ANB (див. рис.2.12); в цілому він є необоротним. На основі нерівності (2.52) для необоротного циклу
Але інтеграл по замкнутому контуру можна записати як суму інтегралів по окремих ділянках, тобто
(за рахунок зміни знаку перед інтегралом у правій частині (2.56) поміняли межі інтегрування).
на основі рівності (2.55), бо ANB – оборотний процес. Тому нерівність (2.56) приймає вигляд
Якби процес АМВ був оборотним, то у (2.57) замість знаку нерівності був би знак рівності (як у (2.55)). Тому для оборотних і необоротних процесів разом можна записати
Остання нерівність – по суті інша форма запису нерівності Клаузіуса і теж є кількісним виразом 2-го начала термодинаміки. У диференціальній формі її можна записати так:
(пам’ятаємо, що знак рівності відповідає оборотним процесам, а знак нерівності – необоротним). Ентропія в останніх нерівностях виступає як міра необоротності процесів. Нехай термодинамічна система ізольована (не має теплообміну з навколишнім середовищем). Тоді
Звідси бачимо, що ентропія ізольованої системи у випадку необоротного процесу зростає, у випадку оборотного – залишається незмінною. Зазначимо, що в ізольованій системі самостійно протікають процеси, котрі ведуть до вирівнювання температури, тиску, густини, концентрації, тобто до стану рівноваги. Тому можна сказати, що ентропія системи в рівноважному стані є максимальною. Твердження про те, що ентропія ізольованої системи не може зменшуватися, носить назву закону зростання ентропії. Математичний запис його – нерівність (2.58). Цей закон є одночасно одним із виразів 2-го начала термодинаміки.
|

 Для оборотного термодинамічного циклу справджується рівність
Для оборотного термодинамічного циклу справджується рівність
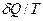 є повним диференціалом деякої функції S, тобто
є повним диференціалом деякої функції S, тобто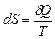 . (2.54)
. (2.54)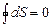 незалежно від виду оборотного процесу), тому кажуть, що ентропія є однією з функцій стану системи. Інакше: приріст ентропії тіла при рівноважному переході його з одного стану (А) в інший (В) визначається лише початковим і кінцевим станами тіла:
незалежно від виду оборотного процесу), тому кажуть, що ентропія є однією з функцій стану системи. Інакше: приріст ентропії тіла при рівноважному переході його з одного стану (А) в інший (В) визначається лише початковим і кінцевим станами тіла: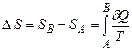 (2.55)
(2.55) .
. або
або  (2.56)
(2.56)
 . (2.57)
. (2.57)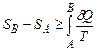 .
.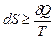
 і остання нерівність зведеться до
і остання нерівність зведеться до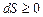 (2.58)
(2.58)


