Спробуємо одержати рівняння дифузії (закон Фіка), виходячи з молекулярно-кінетичних уявлень. Відразу зазначимо, що запропонований нижче розрахунок досить грубий, приблизний і стосується лише газів, в той час як установлений Фіком закон справедливий і для рідин, і для твердих тіл.
 Нехай зміна концентрації молекул вздовж осі z описується функцією n (z). Позначимо число молекул, що пролітають за деякий невеликий проміжок часу
Нехай зміна концентрації молекул вздовж осі z описується функцією n (z). Позначимо число молекул, що пролітають за деякий невеликий проміжок часу  через площадку
через площадку 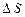 в напрямку осі z, через
в напрямку осі z, через 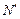 ; те ж число для протилежного напрямку – через
; те ж число для протилежного напрямку – через  (див. рис.2.17). За рахунок різниці цих чисел
(див. рис.2.17). За рахунок різниці цих чисел  створюється потік молекул через поверхню площею
створюється потік молекул через поверхню площею 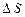 .
.
Будемо виходити зі спрощеної моделі, згідно з якою молекули газу рухаються у трьох взаємно перпендикулярних напрямках так, що в напрямку осі z через нашу площадку за проміжок часу  пролітають молекули, число яких
пролітають молекули, число яких  , а у протилежному напрямку –
, а у протилежному напрямку –  (див. подібну ситуацію в § 2.3). Тут
(див. подібну ситуацію в § 2.3). Тут 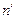 – деяка “ефективна” концентрація молекул зліва від площадки,
– деяка “ефективна” концентрація молекул зліва від площадки,  – справа від неї;
– справа від неї; 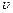 – середня швидкість хаотичного теплового руху молекул газу (газ вважаємо однорідним і всім молекулам приписуємо швидкість
– середня швидкість хаотичного теплового руху молекул газу (газ вважаємо однорідним і всім молекулам приписуємо швидкість 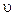 ). В якості
). В якості  візьмемо значення функції n (z) у площині, що на відстані середньої довжини вільного пробігу
візьмемо значення функції n (z) у площині, що на відстані середньої довжини вільного пробігу  від нашої площадки зліва (
від нашої площадки зліва (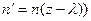 , а в якості
, а в якості 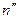 – у площині, що на відстані
– у площині, що на відстані 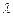 справа (
справа (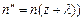 . Тоді маємо
. Тоді маємо
 .
.
Параметр  є дуже малою величиною (див. оцінку її в § 2.18), тому скористаємося означенням похідної
є дуже малою величиною (див. оцінку її в § 2.18), тому скористаємося означенням похідної

і подамо вираз для числа молекул N у вигляді
 . (2.62)
. (2.62)
Остання рівність правильна, якщо зміна функції n(z) на довжині вільного пробігу набагато менша від самої n (z), тобто  . Виконання такої умови ”вимагає” використане нами означення похідної.
. Виконання такої умови ”вимагає” використане нами означення похідної.
Порівняємо тепер співвідношення (2.62) і (2.61). Бачимо, що: 1) ми одержали закон Фіка; 2) попутно маємо явний вигляд коефіцієнта дифузії
 .
.
В межах молекулярно-кінетичних уявлень про газ можна також одержати оцінки в’язкості і теплопровідності:

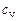 – питома теплоємність газу при постійному об’ємі,
– питома теплоємність газу при постійному об’ємі, 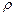 – густина.
– густина.
Коефіцієнти D,  і
і 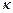 є характеристиками речовини. Одночасно вони залежать від температури і тиску. Результати аналізу цієї залежності для газів подані графічно (рис.2.18).
є характеристиками речовини. Одночасно вони залежать від температури і тиску. Результати аналізу цієї залежності для газів подані графічно (рис.2.18).
 Температурна залежність всіх трьох коефіцієнтів близька до
Температурна залежність всіх трьох коефіцієнтів близька до 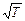 (ясно, що в кожного коефіцієнта своя крива). Залежність від тиску різна в області вакууму і поза нею.
(ясно, що в кожного коефіцієнта своя крива). Залежність від тиску різна в області вакууму і поза нею.

 Нехай зміна концентрації молекул вздовж осі z описується функцією n (z). Позначимо число молекул, що пролітають за деякий невеликий проміжок часу
Нехай зміна концентрації молекул вздовж осі z описується функцією n (z). Позначимо число молекул, що пролітають за деякий невеликий проміжок часу  через площадку
через площадку 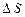 в напрямку осі z, через
в напрямку осі z, через 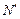 ; те ж число для протилежного напрямку – через
; те ж число для протилежного напрямку – через  (див. рис.2.17). За рахунок різниці цих чисел
(див. рис.2.17). За рахунок різниці цих чисел  створюється потік молекул через поверхню площею
створюється потік молекул через поверхню площею  , а у протилежному напрямку –
, а у протилежному напрямку –  (див. подібну ситуацію в § 2.3). Тут
(див. подібну ситуацію в § 2.3). Тут 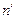 – деяка “ефективна” концентрація молекул зліва від площадки,
– деяка “ефективна” концентрація молекул зліва від площадки,  – справа від неї;
– справа від неї; 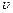 – середня швидкість хаотичного теплового руху молекул газу (газ вважаємо однорідним і всім молекулам приписуємо швидкість
– середня швидкість хаотичного теплового руху молекул газу (газ вважаємо однорідним і всім молекулам приписуємо швидкість 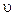 ). В якості
). В якості  візьмемо значення функції n (z) у площині, що на відстані середньої довжини вільного пробігу
візьмемо значення функції n (z) у площині, що на відстані середньої довжини вільного пробігу  від нашої площадки зліва (
від нашої площадки зліва (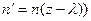 , а в якості
, а в якості 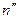 – у площині, що на відстані
– у площині, що на відстані 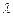 справа (
справа (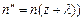 . Тоді маємо
. Тоді маємо .
.
 . (2.62)
. (2.62) . Виконання такої умови ”вимагає” використане нами означення похідної.
. Виконання такої умови ”вимагає” використане нами означення похідної. .
.
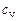 – питома теплоємність газу при постійному об’ємі,
– питома теплоємність газу при постійному об’ємі, 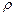 – густина.
– густина. і
і 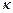 є характеристиками речовини. Одночасно вони залежать від температури і тиску. Результати аналізу цієї залежності для газів подані графічно (рис.2.18).
є характеристиками речовини. Одночасно вони залежать від температури і тиску. Результати аналізу цієї залежності для газів подані графічно (рис.2.18). Температурна залежність всіх трьох коефіцієнтів близька до
Температурна залежність всіх трьох коефіцієнтів близька до 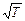 (ясно, що в кожного коефіцієнта своя крива). Залежність від тиску різна в області вакууму і поза нею.
(ясно, що в кожного коефіцієнта своя крива). Залежність від тиску різна в області вакууму і поза нею.


