Характер теплового руху в рідинах. Поверхневий натяг. Явище змочування. Капілярні явища
Рідкий стан речовини є проміжним між газоподібним і кристалічним. Рідина, як і кристал, займає певний об’єм, але як газ, займає форму посудини. В рідині, як у кристалі, молекули розміщені впорядковано (в газах у цьому відношенні – повний хаос). Однак впорядковане розміщення молекул рідини характеризується ближнім порядком: впорядковано розміщені практично лише сусіди кожної молекули. З відстанню порядок порушується. В кристалах існує дальній порядок, у межах значного об’єму. При наявності ближнього порядку структуру рідини називають квазікристалічною. Саме у зв’язку з відсутністю дальнього порядку рідини в основному ізотропні. Молекула рідини якийсь час коливається відносно положення рівноваги (як у вузлі кристалічної решітки твердого тіла), потім вона може перескочити в сусіднє вільне місце. Такий кочовий спосіб життя у всіх молекул рідини. Час осідлості для кожної рідини свій і різко зменшується із збільшенням температури. В останньому випадку збільшується рухливість молекул і, відповідно, зменшується в’язкість рідини. Рівнодійна сил притягання, що діють на молекулу з боку сусідів у товщі рідини, рівна нулю. На молекули, що знаходяться у поверхневому шарі, діють нескомпенсовані зверху сили, направлені в товщу рідини. Ці молекули (а разом і весь поверхневий шар) володіють додатковою потенціальною енергією – вільною енергією поверхні. Стану стійкої рівноваги відповідає мінімум потенціальної енергії, а значить, мінімум площі поверхні. Тому в рідин проявляється тенденція займати форму кулі. Сили, що діють у поверхневому шарі і намагаються скоротити вільну поверхню рідини, направлені по дотичній до поверхні. Їх природа – взаємодія між молекулами. Результати вимірювань показали, що модуль такої сили (
Досліди показують, що поверхня рідини поблизу стінок посудини викривлена. Викривлена вільна поверхня рідини називається меніском. Меніски бувають опуклі та вгнуті. Меніск характеризують крайовим кутом (
Внаслідок дії сил, що скорочують поверхню рідини, викривлений поверхневий шар чинить на рідину тиск 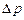 , додатковий по відношенню до зовнішнього тиску. Величина , додатковий по відношенню до зовнішнього тиску. Величина  залежить від коефіцієнта залежить від коефіцієнта 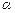 та кривизни поверхні. Розрахуємо додатковий тиск у випадку сферичного меніску. Для цього перетнемо мислено сферичну краплю рідини діаметральною площиною і розділимо тим самим краплю на дві півкулі (рис.2.23). Внаслідок поверхневого натягу обидві півкулі притягуються одна до другої з силою та кривизни поверхні. Розрахуємо додатковий тиск у випадку сферичного меніску. Для цього перетнемо мислено сферичну краплю рідини діаметральною площиною і розділимо тим самим краплю на дві півкулі (рис.2.23). Внаслідок поверхневого натягу обидві півкулі притягуються одна до другої з силою
(на основі (2.66);
В загальному випадку довільної форми поверхні рідини додатковий тиск визначають за формулою Лапласа
Якщо посудина широка, то меніск біля стінки істотної ролі не відіграє. Вільна поверхня рідини в основному горизонтальна. Якщо ж посудина вузька, наприклад, циліндрична тоненька трубка (капіляр), то вся поверхня рідини в ній має форму вгнутого чи опуклого меніска. З достатньою точністю його можна вважати сферичним. Тут додатковий тиск, що виникає під меніском, істотно впливає на рівень рідини в капілярі, сполученому з широкою посудиною з рідиною (рис.2.24). Якщо капіляр змочується рідиною, то в ньому утворюється вгнутий меніск і тиск на рідину стає меншим, ніж у широкій посудині. Рідина піднімається в капілярі (випадок а) на рис.), доки надвишок гідростатичного тиску не скомпенсує лапласівське зменшення тиску під угнутим меніском, тобто доки не справджуватиметься рівність
(див. формули (2.20) та (2.67)). Звідси знаходимо висоту піднімання рідини в капілярі
В розрахунковій формулі для висоти піднімання (опускання) рівня рідини звичайно замість радіуса кривизни меніска (R) вводять радіус капіляра (r). Як видно з рис.2.25,
Капілярні явища суттєві для живлення рослин, клітин живих організмів; їх враховують у будівельній справі, меліорації та інших галузях.
|

 ) прямо пропорційний довжині (
) прямо пропорційний довжині (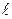 ) контура, що обмежує поверхню рідини
) контура, що обмежує поверхню рідини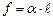 , (2.66)
, (2.66)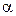 – поверхневий натяг. Числове значення
– поверхневий натяг. Числове значення 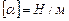 . Фізичний зміст коефіцієнта
. Фізичний зміст коефіцієнта 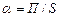 , П – вільна енергія поверхні, S – площа поверхні рідини).
, П – вільна енергія поверхні, S – площа поверхні рідини). ) між змоченою поверхнею стінки і меніском в точці їх дотику. Вгнутому меніску відповідає
) між змоченою поверхнею стінки і меніском в точці їх дотику. Вгнутому меніску відповідає 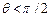 (див. рис.2.22а), кажуть, що рідина змочує стінку. Опуклому меніску відповідає
(див. рис.2.22а), кажуть, що рідина змочує стінку. Опуклому меніску відповідає 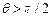 (рис. 2.22б). В цьому випадку кажуть, що рідина не змочує стінку.
(рис. 2.22б). В цьому випадку кажуть, що рідина не змочує стінку. 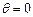 відповідає повне змочування,
відповідає повне змочування, 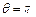 – повне незмочування. Явище змочування спостерігається, якщо сили притягання між молекулами рідини і молекулами стінки переважають сили притягання між молекулами рідини; явище незмочування – якщо переважають сили притягання між молекулами рідини.
– повне незмочування. Явище змочування спостерігається, якщо сили притягання між молекулами рідини і молекулами стінки переважають сили притягання між молекулами рідини; явище незмочування – якщо переважають сили притягання між молекулами рідини.

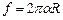
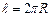 ). Ця сила діє на поверхню площею
). Ця сила діє на поверхню площею 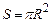 , тому виникає тиск
, тому виникає тиск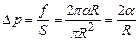 . (2.67)
. (2.67) ,
, де
де  та
та 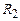 – радіуси кривизни будь-яких двох взаємно перпендикулярних нормальних перерізів поверхні рідини в тому місці, для якого розраховують тиск. Видно, що при
– радіуси кривизни будь-яких двох взаємно перпендикулярних нормальних перерізів поверхні рідини в тому місці, для якого розраховують тиск. Видно, що при 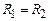 з формули Лапласа випливає вираз (2.67).
з формули Лапласа випливає вираз (2.67).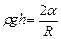
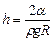 .
. Якщо капіляр не змочується рідиною, то в ньому утворюється опуклий меніск і тиск на рідину стає більшим, ніж у широкій посудині. Рівень рідини в капілярі знижується (випадок б) на рис.). Висота опускання рідини розраховується за тією ж формулою, що й для піднімання.
Якщо капіляр не змочується рідиною, то в ньому утворюється опуклий меніск і тиск на рідину стає більшим, ніж у широкій посудині. Рівень рідини в капілярі знижується (випадок б) на рис.). Висота опускання рідини розраховується за тією ж формулою, що й для піднімання.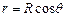 (кути
(кути  та
та  рівні, як кути зі взаємно перпендикулярними сторонами). Остаточно маємо
рівні, як кути зі взаємно перпендикулярними сторонами). Остаточно маємо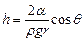 .
.


